Práctica de Suma y Diferencia de Ángulos - Ejercicios

Entendiendo la Tipos de ángulos

Explicación completa con ejemplos

¿Qué es un ángulo?

Definición: Los ángulos se crean en la intersección entre dos rectas. Como se ve en la siguiente ilustración

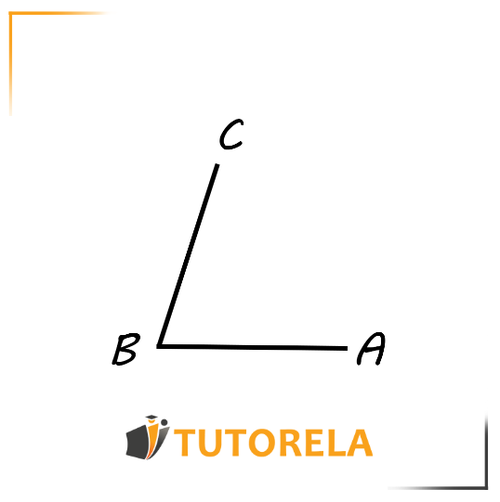
El ángulo en la ilustración es el denominado $AB$ .También podríamos llamarlo ángulo $\sphericalangle ABC$ . Lo importante es que la letra del medio sea la de la intersección de las rectas, que es la abertura entre líneas.

Por ejemplo, en este caso:

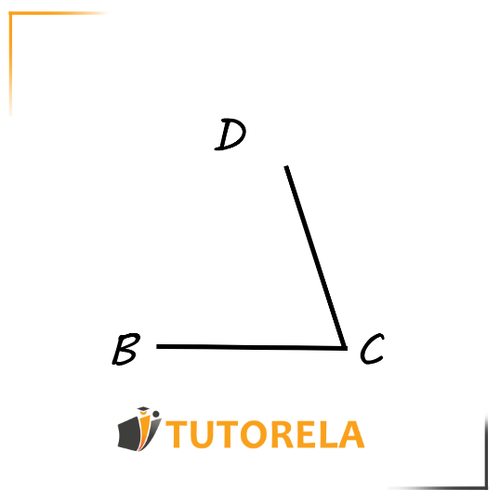
El ángulo es $\sphericalangle BCD$ o $\sphericalangle DCB$ . Ambas señalizaciones son adecuadas para el mismo ángulo.

Por lo general marcaremos el ángulo con un arco del siguiente modo:

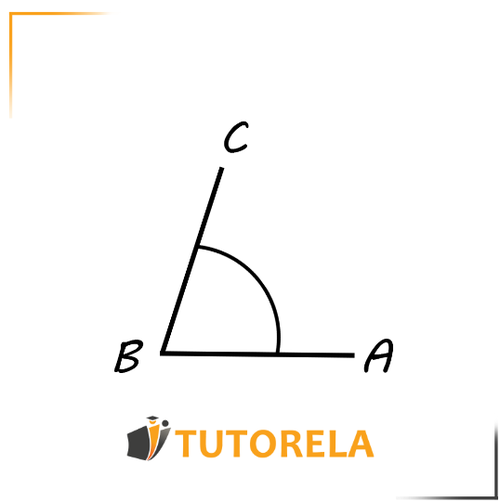
El ángulo marcado es $∡ABC$ . A veces señalaremos los ángulos con letras griegas, por ejemplo:

$α$

o

$β$

Antes del nombre del ángulo deberemos anotar el símbolo de ángulo, así:

$∡$

Junto se ve así:

$∡CBA$

o

$∡α$

A continuación, profundizaremos acerca del tamaño de los ángulos, de los diferentes tipos de ángulos y de aquellos que se generan cuando una recta pasa entre dos rectas paralelas.

Explicación completa

Practicar Tipos de ángulos

Pon a prueba tus conocimientos con más de 27 cuestionarios

ABCD cuadrilátero.

De acuerdo con los datos, calcula el tamaño $$ ∢B $$

ejemplos con soluciones para Tipos de ángulos

Soluciones paso a paso incluidas

Ejercicio #1

Halla la medida del ángulo $\alpha$

Solución Paso a Paso

Recuerda que la suma de los ángulos en un triángulo es igual a 180 grados.

Por lo tanto, usaremos la siguiente fórmula:

$A+B+C=180$

Ahora insertemos los datos conocidos:

$\alpha+50+50=180$

$\alpha+100=180$

Simplificamos la expresión y mantenemos el signo apropiado:

$\alpha=180-100$

$\alpha=80$

Respuesta:

80

Solución en video

Ejercicio #2

Dado el triángulo equilátero, halla X

Solución Paso a Paso

Dado que es un triángulo equilátero, todos los ángulos también son iguales.

Como la suma de los ángulos en un triángulo es 180 grados, cada ángulo es igual a 60 grados. (180:3=60)

De ello se deduce que: $60=8x$

Dividimos ambos lados por 8:

$\frac{60}{8}=\frac{8x}{8}$

$7.5=x$

Respuesta:

7.5

Solución en video

Ejercicio #3

En un triángulo rectángulo, ¿la suma de los dos ángulos no rectos es ?

Solución Paso a Paso

En un triángulo rectángulo hay un ángulo igual a 90 grados, los otros dos ángulos suman 90 grados (180° es la suma de los ángulos en un triángulo)

Por lo tanto, la suma de los dos ángulos no rectos es 90 grados.

$90+90=180$

Respuesta:

90 grados

Solución en video

Ejercicio #4

Dada las medidas de los ángulos: 60,50,70

¿Es posible que estas sean las medidas de los ángulos en cualquier triángulo?

Solución Paso a Paso

Recuerda que la suma de los ángulos en un triángulo es igual a 180 grados.

Sumemos los tres ángulos para ver si su suma es igual a 180:

$60+50+70=180$

Por lo tanto, es posible que estos sean los valores de los ángulos en algún triángulo.

Respuesta:

Posible

Solución en video

Ejercicio #5

¿Puede un triángulo tener más de un ángulo obtuso?

Solución Paso a Paso

Si tratamos de trazar dos ángulos obtusos y conectarlos para formar un triángulo (es decir, solo 3 lados) parece que esto no es posible.

La respuesta es no.

Respuesta:

No

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Tipos de ángulos

¿Cómo se suman dos ángulos adyacentes?

+

Los ángulos adyacentes se suman colocándolos uno junto al otro compartiendo un lado común. Si forman un ángulo llano, su suma siempre será 180°. Por ejemplo, si un ángulo mide 65° y es adyacente a otro de 115°, juntos forman 180°.

¿Cuál es la diferencia entre ángulos correspondientes y alternos?

+

Los ángulos correspondientes están en el mismo lado de la transversal y en la misma posición relativa. Los ángulos alternos están en lados opuestos de la transversal. Ambos tipos son iguales cuando las rectas son paralelas.

¿Cómo resolver problemas de ángulos en rectas paralelas?

+

Para resolver estos problemas: 1) Identifica las rectas paralelas y la transversal, 2) Reconoce los tipos de ángulos (correspondientes, alternos, adyacentes), 3) Aplica las propiedades de igualdad, 4) Plantea ecuaciones usando que los ángulos adyacentes suman 180°.

¿Qué son los ángulos opuestos por el vértice?

+

Son ángulos que se forman cuando dos rectas se cruzan, ubicándose uno frente al otro. Estos ángulos siempre son iguales en medida. Por ejemplo, si dos rectas se cruzan formando un ángulo de 45°, el ángulo opuesto también medirá 45°.

¿Cuándo la suma de ángulos es 180° y cuándo es 360°?

+

La suma es 180° cuando los ángulos son adyacentes formando una línea recta, o cuando son los ángulos internos de un triángulo. La suma es 360° cuando consideramos todos los ángulos alrededor de un punto o los ángulos internos de un cuadrilátero.

¿Cómo identificar si un ángulo es agudo, recto u obtuso en un problema?

+

Un ángulo es agudo si mide menos de 90°, recto si mide exactamente 90°, y obtuso si mide entre 90° y 180°. En los problemas, observa las medidas dadas o calcula usando las propiedades de suma de ángulos.

¿Qué estrategias usar para resolver ecuaciones con ángulos?

+

Estrategias principales: 1) Identifica las relaciones entre ángulos (complementarios, suplementarios, iguales), 2) Plantea ecuaciones usando estas relaciones, 3) Despeja la incógnita paso a paso, 4) Verifica que el resultado tenga sentido geométricamente.

¿Cómo aplicar las propiedades de ángulos en triángulos?

+

En triángulos, la suma de los ángulos internos siempre es 180°. Usa esta propiedad junto con las relaciones de ángulos externos, que equivalen a la suma de los dos ángulos internos no adyacentes. Esto te permite resolver para ángulos desconocidos.