El ángulo exterior de un triángulo es el que se encuentra entre el lado original y la continuación del lado.
El ángulo exterior equivale a la suma de los dos ángulos internos del triángulo que no son adyacentes a él.
Se define así :
Ejercicios de Ángulo Exterior de un Triángulo - Práctica
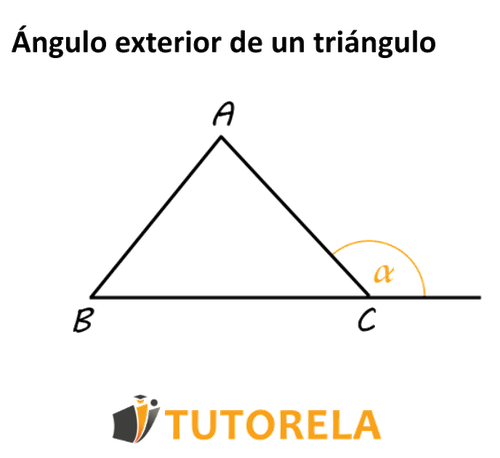
Practica y domina los ángulos exteriores de triángulos con ejercicios paso a paso. Aprende a calcular usando la propiedad fundamental y resuelve problemas reales.
📚Domina los Ángulos Exteriores con Práctica Guiada
- Identifica correctamente ángulos exteriores en cualquier triángulo dado
- Aplica la propiedad: ángulo exterior = suma de dos ángulos internos no adyacentes
- Resuelve problemas calculando ángulos exteriores usando datos conocidos
- Encuentra ángulos internos desconocidos utilizando ángulos exteriores dados
- Diferencia entre ángulos exteriores y ángulos adyacentes en triángulos
- Verifica que la suma de tres ángulos exteriores sea 360 grados
Entendiendo la Ángulo exterior de un triángulo
Explicación completa con ejemplos
Practicar Ángulo exterior de un triángulo
Pon a prueba tus conocimientos con más de 64 cuestionarios
Halla la medida del ángulo \( \alpha \)
ejemplos con soluciones para Ángulo exterior de un triángulo
Soluciones paso a paso incluidas
Ejercicio #1
Dados los dos triángulos, ¿ EC es un lado en uno de los triángulos?
Solución Paso a Paso
Cada triángulo tiene 3 lados, repasaremos el triángulo del lado izquierdo:
Sus lados son: AB,BC,CA
Es decir, en este triángulo el lado EC no existe.
Repasemos el triángulo de la derecha:
Sus lados son: ED,EF,FD
Es decir, en este triángulo el lado EC no existe.
Por lo tanto, EC no es un lado en ninguno de los triángulos.
Respuesta:
No
Solución en video
Ejercicio #2
El triángulo ABC isósceles.
Dada: AD mediana.
¿Cuál es el tamaño del ángulo? ?
Solución Paso a Paso
En un triángulo isósceles, la mediana a la base es también la altura a la base.
Es decir, el lado AD forma un ángulo de 90° con el lado BC.
Es decir, se nos crean dos triángulos rectángulos.
Por lo tanto, el ángulo ADC es igual a 90 grados.
Respuesta:
90
Solución en video
Ejercicio #3
¿Cuál de las siguientes es la altura en el triángulo ABC?
Solución Paso a Paso
Recordemos la definición de altura:
Una altura es una línea recta que desciende del vértice de un triángulo y forma un ángulo de 90 grados con el lado opuesto.
Por lo tanto, el que forma un ángulo de 90 grados es el lado AB con el lado BC
Respuesta:
AB
Solución en video
Ejercicio #4
Dado el triángulo siguiente:
Anote cuál es la altura del triángulo ABC.
Solución Paso a Paso
Una altura en un triángulo es el segmento que une el vértice y el lado opuesto, de tal manera que el segmento forma un ángulo de 90 grados con el lado.
Si observamos el dibujo, podemos notar que el teorema anterior es cierto para la recta AE que cruza BC y forma un ángulo de 90 grados, sale del vértice A y por lo tanto es la altura del triángulo.
Respuesta:
AE
Solución en video
Ejercicio #5
¿Puede un triángulo tener más de un ángulo obtuso?
Solución Paso a Paso
Si tratamos de trazar dos ángulos obtusos y conectarlos para formar un triángulo (es decir, solo 3 lados) parece que esto no es posible.
La respuesta es no.
Respuesta:
No
Solución en video
Preguntas Frecuentes
¿Qué es un ángulo exterior de un triángulo?
+Un ángulo exterior de un triángulo es el ángulo que se forma entre un lado original del triángulo y la prolongación (continuación) de otro lado. Este ángulo siempre está ubicado fuera del triángulo y nunca entre dos prolongaciones de lados.
¿Cómo se calcula un ángulo exterior de un triángulo?
+Para calcular un ángulo exterior, utiliza la propiedad fundamental: el ángulo exterior es igual a la suma de los dos ángulos internos del triángulo que NO son adyacentes a él. Por ejemplo, si los ángulos internos no adyacentes miden 60° y 40°, el ángulo exterior será 60° + 40° = 100°.
¿Cuál es la diferencia entre ángulo exterior y ángulo adyacente?
+Un ángulo exterior está fuera del triángulo formado por un lado y su prolongación. Un ángulo adyacente está junto al ángulo exterior y ambos suman 180°. El ángulo adyacente es complementario al exterior, mientras que el exterior equivale a la suma de dos ángulos internos específicos.
¿Cuántos ángulos exteriores tiene un triángulo?
+Un triángulo tiene 6 ángulos exteriores en total: 2 en cada vértice (uno a cada lado del vértice). Sin embargo, en cada vértice solo se considera uno de ellos para resolver problemas, ya que los dos ángulos exteriores en el mismo vértice son iguales.
¿Por qué la suma de ángulos exteriores es 360 grados?
+La suma de los tres ángulos exteriores de cualquier triángulo siempre es 360°. Esto se debe a que cada ángulo exterior equivale a la suma de dos ángulos internos no adyacentes, y al sumar los tres exteriores, cada ángulo interno se cuenta exactamente dos veces: 2 × 180° = 360°.
¿Cómo resolver ejercicios con ángulos exteriores paso a paso?
+Sigue estos pasos: 1) Identifica el ángulo exterior en el diagrama, 2) Determina cuáles son los dos ángulos internos NO adyacentes a él, 3) Aplica la fórmula: ángulo exterior = suma de los dos ángulos internos no adyacentes, 4) Sustituye los valores conocidos y resuelve la ecuación.
¿Qué errores comunes se cometen con ángulos exteriores?
+Los errores más frecuentes incluyen: confundir el ángulo exterior con el adyacente interno, sumar los ángulos internos incorrectos (usar el adyacente en lugar de los no adyacentes), y no identificar correctamente cuál es la prolongación del lado versus el lado original del triángulo.
¿En qué situaciones reales se usan los ángulos exteriores?
+Los ángulos exteriores se aplican en arquitectura para calcular inclinaciones de techos, en topografía para medir terrenos triangulares, en navegación para determinar rumbos, y en ingeniería civil para diseñar estructuras con formas triangulares como puentes y torres.