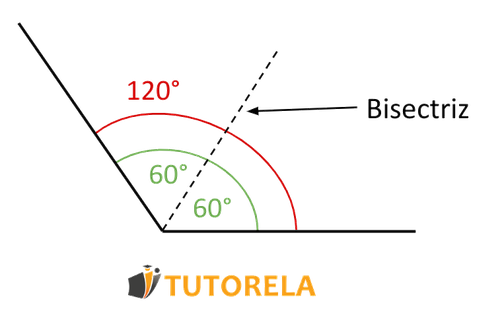
Una bisectriz es un segmento de recta que pasa por el vértice de un ángulo y lo divide en dos ángulos iguales.
La bisectriz puede aparecer en un triángulo, paralelogramo, rombo y en otras figuras geométricas.
Por ejemplo, una bisectriz que pasa a través de un ángulo de grados creará dos ángulos de grados cada uno.
ABCD Deltoide.
Calcula el tamaño del ángulo
\( ∢DAC=\text{?} \)
Dado que BD es una bisectriz, ¿cuál es la medida del ángulo ABC?
Dado que a es una bisectriz, halla el ángulo \( \alpha \)
¿Cuál de las siguientes figuras tiene una bisectriz?
Dado que a es una bisectriz, halla el ángulo \( \alpha \)
ABCD Deltoide.
Calcula el tamaño del ángulo
Como sabemos que ABCD es un deltoide, AC es la bisectriz de un ángulo y por lo tanto:
Ahora nos enfocamos en el triangulo BAD y calculamos la suma de los ángulos ya que sabemos que la suma de los ángulos en el triángulo es 180 grados:
Dividimos las dos secciones por 6:
Ahora podemos calcular el ángulo DAC:
30
Dado que BD es una bisectriz, ¿cuál es la medida del ángulo ABC?
130
Dado que a es una bisectriz, halla el ángulo
60
¿Cuál de las siguientes figuras tiene una bisectriz?
Dado que a es una bisectriz, halla el ángulo
45
Dado:
\( ∢\text{ABD}=15 \)
BD bisectriz.
Calcule el tamaño \( ∢\text{ABC} \)
\( \)
Dado:
\( ∢\text{ABC}=90 \)
\( ∢DBC=45 \)
¿Es BD una bisectriz?
Dado:
\( ∢ABC=120 \)
\( ∢ABD=60 \)
Elija la respuesta correcta
Dado BO bisectríz \( ∢ABD \)
\( ∢\text{ABD}=85 \)
Calcule el tamaño de
\( ∢ABO \)
\( ∢DBC=90° \)
BE divide en dos a\( ∢\text{DBA} \)
Encuentra el valor \( \alpha \)
Dado:
BD bisectriz.
Calcule el tamaño
30
Dado:
¿Es BD una bisectriz?
Si
Dado:
Elija la respuesta correcta
BD bisectriz
Dado BO bisectríz
Calcule el tamaño de
42.5
BE divide en dos a
Encuentra el valor
45
Dado:
\( ∢\text{ABD}=90 \)
CB Bisectriz \( ∢\text{ABD} \)\( ∢\text{CBD}=\alpha \)
Calcule el tamaño \( ∢ABC \)
Dado que a es la bisectriz de
\( ∢BAC = 80° \)
Halla el ángulo \( \alpha \)
\( ∢ABC\text{ }=130 \)
Dado que a es una bisectriz, halla el ángulo \( \alpha \)
Dado que BD es una bisectriz, ¿cuál es el valor del ángulo ABC?
Dado BE bisectríz \( ∢\text{FBD} \)
\( ∢\text{FBE}=25 \)
Calcule el tamaño \( ∢\text{EBD} \)
Dado:
CB Bisectriz
Calcule el tamaño
45
Dado que a es la bisectriz de
Halla el ángulo
40
Dado que a es una bisectriz, halla el ángulo
65
Dado que BD es una bisectriz, ¿cuál es el valor del ángulo ABC?
80
Dado BE bisectríz
Calcule el tamaño
25