Podemos añadir ángulos y obtener el resultado de su suma y también restarlos y obtener la diferencia entre ellos.
Aún si los ángulos no tienen ningún número aprenderemos cómo representar su suma o resta y llegar al resultado correcto.
Ejercicios de Suma y Diferencia de Ángulos - Práctica Online
Practica suma y diferencia de ángulos con ejercicios interactivos. Aprende a calcular ángulos adyacentes, complementarios y suplementarios paso a paso.
📚Domina la Suma y Diferencia de Ángulos con Ejercicios Prácticos
- Calcular la suma de ángulos que comparten el mismo vértice
- Determinar ángulos faltantes usando propiedades de resta angular
- Resolver problemas con ángulos en triángulos y rectas paralelas
- Aplicar la regla fundamental: el todo es la suma de sus partes
- Identificar y nombrar correctamente ángulos en figuras geométricas
- Trabajar con ángulos adyacentes, complementarios y suplementarios
Entendiendo la Suma y diferencia de angulos
Explicación completa con ejemplos
Suma y diferencia de ángulos
Suma de ángulos
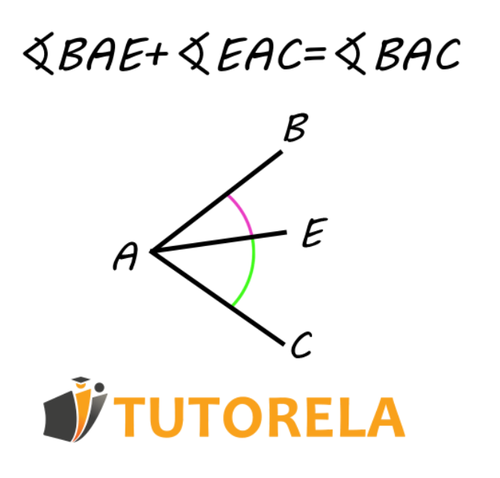
Para encontrar la suma de ángulos éstos tienen que tener un vértice en común.
Diferencia entre ángulos
Del mismo modo que hemos sumado los ángulos también podremos restar uno de otro.
Practicar Suma y diferencia de angulos
Pon a prueba tus conocimientos con más de 27 cuestionarios
Dados los ángulos entre paralelas:
¿Cuál es el valor de X?
ejemplos con soluciones para Suma y diferencia de angulos
Soluciones paso a paso incluidas
Ejercicio #1
Halla la medida del ángulo
Solución Paso a Paso
Recuerda que la suma de los ángulos en un triángulo es igual a 180 grados.
Por lo tanto, usaremos la siguiente fórmula:
Ahora insertemos los datos conocidos:
Simplificamos la expresión y mantenemos el signo apropiado:
Respuesta:
80
Solución en video
Ejercicio #2
Dados los tres ángulos:
Ángulo A es igual a 56°
Ángulo B es igual a 89°
Ángulo C es igual a 17°
¿Estos ángulos pueden componer un triángulo?
Solución Paso a Paso
Sumamos los tres ángulos para ver si son iguales a 180 grados:
La suma de los ángulos dados no es igual a 180, por lo que no pueden formar un triángulo.
Respuesta:
No
Solución en video
Ejercicio #3
Dados los tres ángulos:
Ángulo A es igual a 30°
Ángulo B es igual a 60°
Ángulo C es igual a 90°
¿Estos ángulos pueden componer un triángulo?
Solución Paso a Paso
Sumamos los tres ángulos para ver si son iguales a 180 grados:
La suma de los ángulos es igual a 180, por lo que pueden formar un triángulo.
Respuesta:
Si
Solución en video
Ejercicio #4
Dados los tres ángulos:
Ángulo A es igual a 90°
Ángulo B es igual a 115°
Ángulo C es igual a 35°
¿Estos ángulos pueden componer un triángulo?
Solución Paso a Paso
Sumamos los tres ángulos para ver si son iguales a 180 grados:
La suma de los ángulos dados no es igual a 180, por lo que no pueden formar un triángulo.
Respuesta:
No
Solución en video
Ejercicio #5
Dada las medidas de los ángulos: 60,50,70
¿Es posible que estas sean las medidas de los ángulos en cualquier triángulo?
Solución Paso a Paso
Recuerda que la suma de los ángulos en un triángulo es igual a 180 grados.
Sumemos los tres ángulos para ver si su suma es igual a 180:
Por lo tanto, es posible que estos sean los valores de los ángulos en algún triángulo.
Respuesta:
Posible
Solución en video
Preguntas Frecuentes
¿Cómo se suman dos ángulos que comparten el mismo vértice?
+Para sumar ángulos deben tener un vértice común. Si el ángulo ∠BAC contiene los ángulos ∠BAE y ∠EAC, entonces ∠BAC = ∠BAE + ∠EAC. Es importante identificar correctamente los rayos que forman cada ángulo.
¿Cuál es la diferencia entre suma y resta de ángulos?
+La suma combina ángulos adyacentes para formar un ángulo mayor, mientras que la resta encuentra un ángulo faltante cuando conocemos el ángulo total y uno de sus componentes. Ambas operaciones se basan en que el todo es igual a la suma de sus partes.
¿Qué condiciones deben cumplir los ángulos para poder sumarlos?
+Los ángulos deben: 1) Compartir el mismo vértice, 2) Ser adyacentes (uno junto al otro sin superponerse), 3) No tener interior común. Solo así podemos aplicar la propiedad aditiva de ángulos correctamente.
¿Cómo calcular un ángulo faltante en un triángulo?
+Usa la propiedad de que la suma de ángulos internos de un triángulo es 180°. Si conoces dos ángulos, resta su suma de 180° para encontrar el tercero: ángulo faltante = 180° - ángulo1 - ángulo2.
¿Qué son los ángulos complementarios y suplementarios?
+Los ángulos complementarios suman 90° (forman un ángulo recto), mientras que los suplementarios suman 180° (forman una línea recta). Estas relaciones son fundamentales para resolver problemas de suma y diferencia angular.
¿Cómo identificar correctamente los ángulos en una figura?
+Nombra los ángulos usando tres puntos: el vértice al centro y un punto de cada rayo. Por ejemplo, ∠ABC tiene vértice en B. Lee la figura cuidadosamente para identificar qué ángulos son parte de otros ángulos mayores.
¿Qué errores comunes ocurren al sumar y restar ángulos?
+Los errores más frecuentes incluyen: 1) Confundir el orden de los puntos al nombrar ángulos, 2) No verificar que los ángulos sean adyacentes, 3) Olvidar que la suma de ángulos en un triángulo es 180°, 4) No identificar correctamente el ángulo resultante.
¿Cómo resolver problemas con rectas paralelas y ángulos?
+Usa las propiedades de ángulos formados por rectas paralelas: ángulos correspondientes son iguales, ángulos alternos internos son iguales, y ángulos co-internos suman 180°. Identifica primero qué tipo de ángulos tienes antes de aplicar suma o resta.