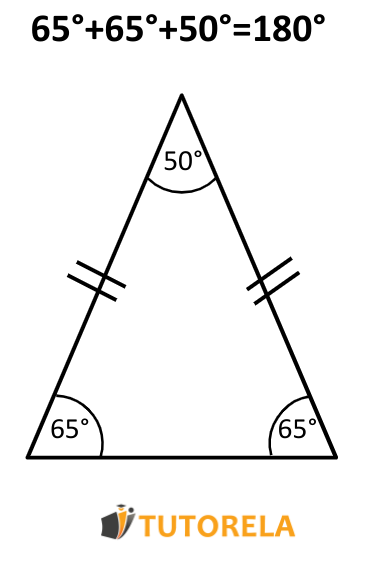
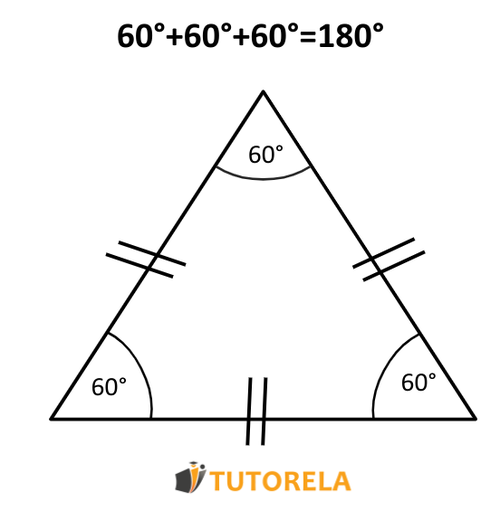
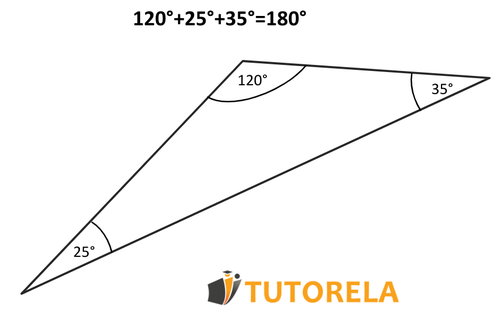
La suma de los ángulos internos de un triángulo es grados, es decir, si sumamos los tres ángulos de cualquier triángulo que elijamos, el resultado siempre será grados. Esto quiere decir que, si sabemos la medida de dos ángulos de un triángulo siempre podremos calcular, con facilidad, la medida del tercero: primero sumaremos los dos ángulos que conocemos y luego le restamos a el resultado de la suma de los dos ángulos. El resultado de esta resta nos dará la medida del tercer ángulo del triángulo.
Por ejemplo, dado un triángulo con dos ángulos interiores conocidos de y grados, se nos pide descubrir la medida del tercer ángulo. Primero sumaremos más teniendo como resultado grados. Ahora restamos de , obteniendo como resultado grados. En otras palabras, el tercer ángulo del triángulo equivale a grados.
La propiedad anterior también la podemos encontrar con el nombre de teorema de los ángulos interiores de un triángulo y nos puede ayudar a resolver problemas que involucren a los ángulos interiores de un triángulo sin importar si es equilátero, isósceles o escaleno.