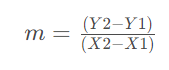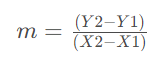Ejercicios de Función Lineal y=mx+b con Soluciones

Practica ejercicios de función lineal y=mx+b. Aprende a identificar pendiente, intersección y graficar rectas. Problemas resueltos paso a paso.

📚Domina la Función Lineal y=mx+b con Ejercicios Prácticos

Identificar la pendiente m y la intersección b en ecuaciones lineales
Determinar si un punto dado pertenece a una función lineal específica
Graficar funciones lineales usando tabla de valores y dos puntos
Calcular la pendiente entre dos puntos usando la fórmula m=(Y2-Y1)/(X2-X1)
Interpretar funciones crecientes, decrecientes y horizontales según el valor de m
Resolver problemas de intersección con los ejes X e Y

Entendiendo la Función lineal y=mx+b

Explicación completa con ejemplos

La función lineal $y=mx+b$ en realidad representa un gráfico de una línea recta que tiene un punto de intersección con el eje $Y$ vertical.

$m$ representa la pendiente.
Cuando $m$ Positivo: la pendiente es positiva: la recta es ascendente.
Cuando $m$ Negativo: la pendiente es negativa: la recta es descendente.
Cuando $m = 0$ La pendiente es igual a $0$ La recta es paralela al eje $X$

$b$ representa el punto de intersección de la recta con el eje $Y$ .
Si $b=0$ Entonces la recta pasará por el origen de las coordenadas, es decir, el punto $\left(0,0\right)$

Un ejercicio sobre la función lineal

Se nos da una función lineal $y=3x+4$

Se nos pide que interpretemos los valores $3$ y $4$ y se traza la gráfica de la función.

Primero, parece que $m=3$ , es decir, $3$ representa la pendiente de la recta (o de la función).

$b=4$ Es decir, la línea corta el eje vertical. $Y$ sobre $4$

Para trazar el gráfico, todo lo que necesitamos es $2$ puntos.
Reemplazamos y obtenemos:

1.a - Un ejercicio sobre la función lineal

Ahora marcaremos los dos puntos en el sistema de coordenadas y los conectaremos.
Si observamos el gráfico, podemos probar que el gráfico interseca el eje $Y$ en el valor de $4$ .

Explicación completa

Practicar Función lineal y=mx+b

Pon a prueba tus conocimientos con más de 13 cuestionarios

Para la función frente a ti, ¿la pendiente es?

ejemplos con soluciones para Función lineal y=mx+b

Soluciones paso a paso incluidas

Ejercicio #1

Dada la función lineal:

$y=x-4$

¿Cuál es la tasa de cambio de la función?

Solución Paso a Paso

Recordemos que la tasa de cambio es igual a la pendiente.

En este caso, la pendiente es:

$m=1$

Respuesta:

$m=1$

Solución en video

Ejercicio #2

Halle la pendiente de la recta que pasa por los puntos $(4,1),(2,5)$

Solución Paso a Paso

Recuerda la fórmula para calcular la pendiente mediante los puntos:

Ahora, reemplazamos los datos en la fórmula:

$\frac{(5-1)}{(2-4)}=\frac{4}{-2}=-2$

Respuesta:

-2

Solución en video

Ejercicio #3

Halle la pendiente de la recta que pasa por los puntos $(0,0),(-8,2)$

Solución Paso a Paso

Para resolver la consigna, recuerda la fórmula para hallar la pendiente mediante dos puntos

Ahora, reemplazamos los puntos dados en el cálculo:

$\frac{(0-2)}{(0-(-8)}=\frac{-2}{8}=-\frac{1}{4}$

Respuesta:

$-\frac{1}{4}$

Solución en video

Ejercicio #4

Elija la respuesta correcta para la función.

$y=-x+1$

Solución Paso a Paso

Comencemos con la opción A

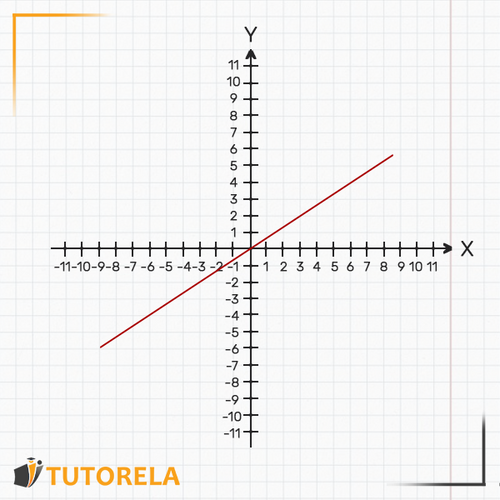
En una función lineal, para verificar si las funciones son paralelas, debe verificar si su pendiente es la misma.

y = ax+b

La pendiente es a

En la fórmula original:

y = -x+1

La pendiente es 1

En la opción A no hay a en absoluto, lo que significa que es igual a 1, lo que significa que la pendiente no es la misma y la opción es incorrecta.

Opción B:

Para comprobar si la función pasa por los puntos, intentaremos colocarlos en la función:

-1 = -(-2)+1

-1 = 2+1

-1 = 3

Los puntos no coinciden, y por lo tanto la función no pasa por este punto.

Opción C:

Reordenamos la función, de una manera que sea más conveniente:

y = -1-x

y = -x-1

Puedes ver que la pendiente en la función es la misma que la encontramos para la función original (-1), ¡así que esta es la solución!

Opción D:

Cuando la pendiente es negativa, la función es decreciente, como la pendiente es -1, la función es negativa y esta respuesta es incorrecta.

Respuesta:

_{La gráfica es paralela a la gráfica de la función}

_^$y=-1-x$

Solución en video

Ejercicio #5

Para la función frente a ti, ¿la pendiente es?

Solución Paso a Paso

Respuesta:

Pendiente negativa

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Función lineal y=mx+b

¿Qué significa m y b en la función lineal y=mx+b?

En la función lineal y=mx+b, 'm' representa la pendiente de la recta (qué tan inclinada está) y 'b' representa el punto donde la recta interseca el eje Y. Por ejemplo, en y=3x+4, la pendiente es 3 y la intersección con el eje Y es 4.

¿Cómo saber si una función lineal es creciente o decreciente?

Observa el valor de la pendiente m: Si m > 0 (positivo), la función es creciente. Si m < 0 (negativo), la función es decreciente. Si m = 0, la función es constante (horizontal).

¿Cómo graficar una función lineal paso a paso?

Para graficar y=mx+b: 1) Marca el punto (0,b) en el eje Y, 2) Usa la pendiente m para encontrar otro punto, 3) Conecta los puntos con una línea recta. También puedes crear una tabla con al menos 3 valores de x y calcular sus correspondientes valores de y.

¿Cómo verificar si un punto está en una función lineal?

Sustituye las coordenadas del punto (x,y) en la ecuación. Si al reemplazar x obtienes el mismo valor de y, entonces el punto pertenece a la función. Por ejemplo, para verificar si (2,10) está en y=3x+4: 3(2)+4 = 10 ✓

¿Qué pasa cuando b=0 en la función lineal?

Cuando b=0, la función se convierte en y=mx, lo que significa que la recta pasa por el origen de coordenadas (0,0). La recta interseca ambos ejes en el punto (0,0).

¿Cómo calcular la pendiente si tengo dos puntos?

Usa la fórmula: m = (Y2-Y1)/(X2-X1). Por ejemplo, con los puntos (1,7) y (3,13): m = (13-7)/(3-1) = 6/2 = 3. Esta pendiente indica que por cada unidad que aumenta x, y aumenta 3 unidades.

¿Cuáles son los errores más comunes al graficar funciones lineales?

Los errores más frecuentes incluyen: confundir la pendiente con la intersección, no marcar correctamente el punto (0,b), usar escala incorrecta en los ejes, y no verificar que los puntos calculados estén alineados en una recta.

¿Cómo interpretar una pendiente negativa en problemas reales?

Una pendiente negativa indica una relación inversa: cuando una variable aumenta, la otra disminuye. Por ejemplo, en y=-2x+100, si x representa tiempo y y representa combustible, significa que cada unidad de tiempo consume 2 unidades de combustible.

Continúa tu viaje matemático

Domina primero la Función lineal y=mx+b, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas que se aprenden en secciones posteriores

Función lineal Positividad y negatividad de una función lineal Hallar ecuación lineal Representación gráfica de una función que representa una proporcionalidad directa Representación de fenómenos usando funciones lineales

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Aumento y disminución en relación con la pendiente Calcular la pendiente a partir de dos puntos Calcular la pendiente a partir de una tabla Convirtiendo entre gráficos y ecuaciones Determinar la pendiente de una función lineal Determinar si la pendiente en el gráfico es positiva o negativa Entendiendo el concepto de pendiente Uso de la pendiente para problemas geométricos