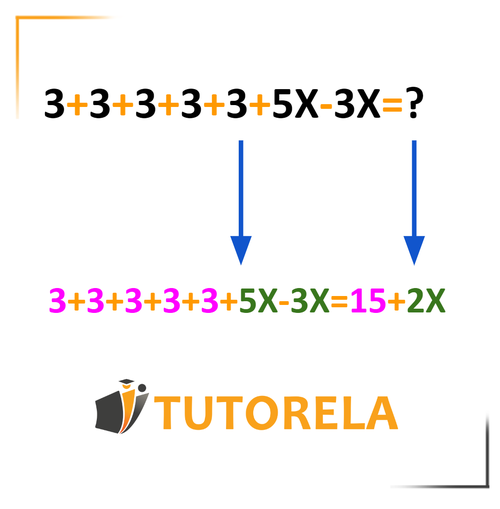
La simplificación de elementos consiste en crear una expresión equivalente escrita de manera más corta y sencilla en la que aunamos todos los elementos semejantes.
Por ejemplo, la expresión
Después de haberla simplificado , quedaría:
Lo que hemos hecho es crear dos grupos: cifras e incógnitas, es decir,
y
Hemos aunado de manera sencilla en dos únicos elementos
\( 7a+8b+4a+9b=\text{?} \)
Para resolver el ejercicio, ordenaremos los números usando la propiedad sustitutiva.
Para continuar, recordaremos una regla importante:
1. Es imposible sumar o restar números con incógnitas.
Es decir, no podemos restarle 7 a 8X, por ejemplo...
Resolvemos según el orden de las operaciones aritméticas, de izquierda a derecha:
Recuerda, estos dos números no se pueden sumar ni restar, por lo que el resultado es:
Respuesta:
Reconoceremos que en la ecuación tenemos dos tipos de elementos: algunos con la incógnita X y otros sin ella.
Sumamos cada uno de ellos por separado:
Por lo tanto, el resultado es:
Respuesta:
Es importante recordar que cuando tenemos números ordinarios e incógnitas, es imposible sumarlos o restarlos entre sí.
Agrupamos los elementos:
29.2a + 2.3 + 8a =
Y en este ejercicio, ¡esta es la solución!
Se puede continuar buscando el valor de a.
Pero en este caso no hay necesidad.
Respuesta:
Respuesta:
Respuesta: