Variables y Expresiones Algebraicas - Ejercicios y Problemas

Practica variables y expresiones algebraicas con ejercicios paso a paso. Aprende a evaluar, simplificar y resolver problemas algebraicos básicos de forma fácil.

📚Domina las Variables y Expresiones Algebraicas con Práctica Guiada

Identifica variables y constantes en expresiones algebraicas simples
Evalúa expresiones algebraicas sustituyendo valores numéricos específicos
Simplifica expresiones combinando términos semejantes correctamente
Traduce problemas escritos a expresiones algebraicas usando variables
Aplica propiedades distributivas para expandir expresiones algebraicas
Resuelve problemas del mundo real usando variables y expresiones

Entendiendo la Expresiones equivalentes / Expresiones algebraicas equivalentes

Explicación completa con ejemplos

En anteriores artículos, hablamos sobre que es una expresión algebraica y el valor numérico de las expresiones algebraicas. Hoy estudiaremos las expresiones equivalentes.

Las expresiones equivalentes son expresiones algebraicas (dos o más) que representan la misma cantidad. Éstas pueden tener una estructura distinta, pero su valor numérico será el mismo.

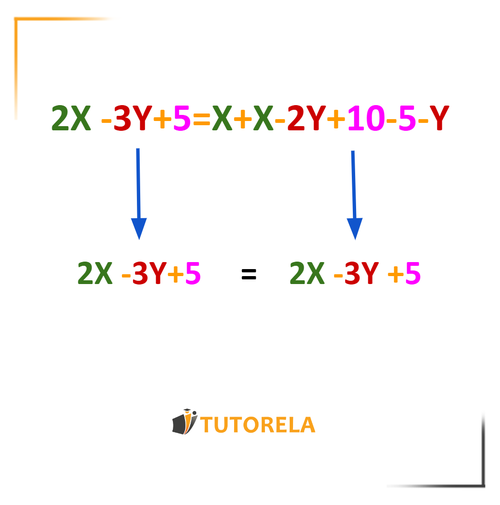
Por ejemplo, en la siguiente igualdad, en ambos lados representan la misma cantidad:

$9X=3X+6X$

Otro ejemplo con 2 variables. Simplificando las expresiones de ambos lados de la igualdad. podemos darnos cuenta que en ambas tenemos $2X-3Y+5$ , es decir, las expresiones son equivalentes.

$2X-3Y+5=X+X-2Y+10-5-Y$

Explicación completa

Practicar Expresiones equivalentes / Expresiones algebraicas equivalentes

Pon a prueba tus conocimientos con más de 14 cuestionarios

¿Las expresiones son iguales o no?

$0.5x\times1$

$$ 0.5x+0 $$

ejemplos con soluciones para Expresiones equivalentes / Expresiones algebraicas equivalentes

Soluciones paso a paso incluidas

Ejercicio #1

$108-8x+32+4x=\text{?}$

Solución Paso a Paso

Reconoceremos que en la ecuación tenemos dos tipos de elementos: algunos con la incógnita X y otros sin ella.

Sumamos cada uno de ellos por separado:

$108+32=140$

$-8x+4x=-4x$

Por lo tanto, el resultado es:

$140-4x$

Respuesta:

$140-4x$

Solución en video

Ejercicio #2

$18x-7+4x-9-8x=\text{?}$

Solución Paso a Paso

Para resolver el ejercicio, ordenaremos los números usando la propiedad sustitutiva.

$18x-8x+4x-7-9=$

Para continuar, recordaremos una regla importante:

1. Es imposible sumar o restar números con incógnitas.

Es decir, no podemos restarle 7 a 8X, por ejemplo...

Resolvemos según el orden de las operaciones aritméticas, de izquierda a derecha:

$18x-8x=10x$ $10x+4x=14x$ $-7-9=-16$ Recuerda, estos dos números no se pueden sumar ni restar, por lo que el resultado es:

$14x-16$

Respuesta:

$14x-16$

Solución en video

Ejercicio #3

$7.3\cdot4a+2.3+8a=\text{?}$

Solución Paso a Paso

Es importante recordar que cuando tenemos números ordinarios e incógnitas, es imposible sumarlos o restarlos entre sí.

Agrupamos los elementos:

$7.3×4a + 2.3 + 8a =$

$29.2a + 2.3 + 8a =$

$37.2a + 2.3$

Y en este ejercicio, ¡esta es la solución!

Se puede continuar buscando el valor de a.

Pero en este caso no hay necesidad.

Respuesta:

$37.2a+2.3$

Solución en video

Ejercicio #4

¿Las expresiones son iguales o no?

$18x$

$2+9x$

Solución Paso a Paso

Respuesta:

Solución en video

Ejercicio #5

¿Las expresiones son iguales o no?

$20x$

$2\times10x$

Solución Paso a Paso

Respuesta:

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Expresiones equivalentes / Expresiones algebraicas equivalentes

¿Qué es una variable en matemáticas?

Una variable es un símbolo (generalmente una letra como x, y, o z) que representa un número desconocido o que puede cambiar de valor. Las variables nos permiten escribir fórmulas y resolver problemas matemáticos de manera general.

¿Cómo se evalúa una expresión algebraica?

Para evaluar una expresión algebraica, sustituye cada variable por su valor numérico dado y realiza las operaciones matemáticas siguiendo el orden correcto. Por ejemplo, si x = 3 en la expresión 2x + 5, el resultado sería 2(3) + 5 = 11.

¿Cuál es la diferencia entre términos semejantes y diferentes?

Los términos semejantes tienen las mismas variables con los mismos exponentes, solo difieren en el coeficiente numérico. Los términos diferentes tienen variables distintas o exponentes diferentes. Solo los términos semejantes se pueden combinar sumando o restando sus coeficientes.

¿Cómo se simplifica una expresión algebraica?

Para simplificar una expresión algebraica sigue estos pasos: 1. Elimina paréntesis usando la propiedad distributiva 2. Identifica términos semejantes 3. Combina términos semejantes sumando o restando coeficientes 4. Ordena los términos de mayor a menor grado

¿Qué son los coeficientes en álgebra?

Los coeficientes son los números que multiplican a las variables en una expresión algebraica. En el término 5x, el coeficiente es 5. Si no hay número visible, como en 'x', el coeficiente es 1.

¿Cómo traducir palabras a expresiones algebraicas?

Identifica las palabras clave y sus significados matemáticos: • 'Más que' o 'suma' → + • 'Menos que' o 'diferencia' → - • 'Producto' o 'veces' → × • 'Cociente' o 'dividido entre' → ÷ • 'Un número' → variable (x, y, etc.)

¿Cuáles son los errores más comunes con expresiones algebraicas?

Los errores más frecuentes incluyen: • Combinar términos que no son semejantes • Olvidar aplicar el signo negativo a todos los términos • Confundir coeficientes con exponentes • No respetar el orden de las operaciones al evaluar

¿Para qué sirven las expresiones algebraicas en la vida real?

Las expresiones algebraicas tienen múltiples aplicaciones prácticas: calcular costos totales en compras, determinar distancias y velocidades, resolver problemas de finanzas personales, y modelar situaciones en ciencias e ingeniería. Son la base para resolver problemas del mundo real de manera sistemática.

Continúa tu viaje matemático

Domina primero la Expresiones equivalentes / Expresiones algebraicas equivalentes, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas que se aprenden en secciones posteriores

Incógnitas y expresiones algebraicas Multiplicación de expresiones algebraicas Simplificación de elementos semejantes El valor numérico en expresiones algebraicas Transposición de términos y dominio de ecuaciones de una incógnita.Dominio de una función

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Aplicación de la fórmula Comparación con una expresión existente Completar los números faltantes Denominadores comunes con variables Denominadores diferentes con variables Números decimales Propiedad distributiva extendida Solo suma y resta Usando formas geométricas adicionales Uso de fracciones Uso de potencias