La transposición de términos implica pasar los términos de una ecuación de un miembro a otro. De hecho, se trata de un grupo de números que, según las reglas matemáticas, están permitidos para colocarlos en lugar de la incógnita (o variable) dentro de una ecuación. El concepto transposición de términos es especialmente concerniente a las ecuaciones con fracciones o raíces cuadradas para poder encontrar el dominio de la ecuación.
En ciertos casos debemos prestar atención a la transposición de términos:
- En caso de fracción el denominador no puede ser igual a cero.
- En caso de raíz cuadrada, el radicando no puede ser negativo.
Esto significa que, en dichos casos, no es suficiente resolver la ecuación sino, se debe corroborar si la solución dada es sustentable o tiene sentido en los números reales.
¿Cómo se encuentra el dominio de una ecuación de una incógnita?
1. En ecuaciones con fracciones encontraremos el dominio igualando el denominador a cero.
El valor o los valores que causan que el denominador sea igual a cero se encuentran fuera del dominio de la ecuación.
- En una ecuación con raíz los valores que causan que la raíz sea negativa se encuentran fuera del dominio de la ecuación.
A continuación podemos ver un ejemplo de cómo encontrar el dominio de una ecuación usando la transposición de términos:
Ejemplo :
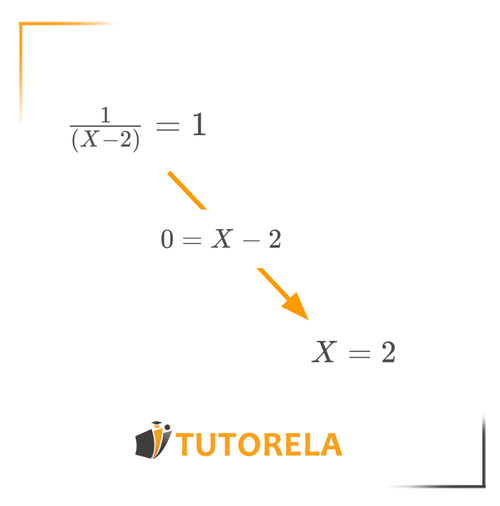
Se trata de una ecuación con fracción en la que la incógnita aparece en el denominador. El denominador no puede ser cero, por lo tanto la expresión no está bien definida:
Usando la transposición de términos podemos despejar la incógnita y obtenemos:
Por lo tanto, el dominio de la función son todos los números reales excepto cuando .