Expresiones equivalentes / Expresiones algebraicas equivalentes

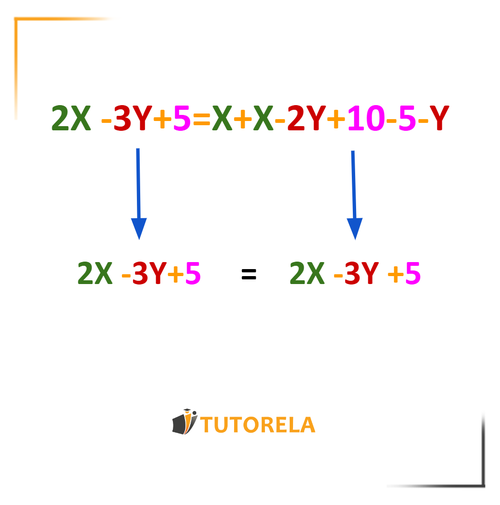
A continuación presentamos una serie de ejercicios de Las expresiones equivalentes

Aquí te dejamos algunos ejemplos:

• $1+1=2$
• $2-0=2$
• $7X=2X+5X$
• $4X\times\left(2+3\right)=8X+12X$
• $8X+12X=20X$

Escribe una expresión equivalente a cada una de las expresiones siguientes:

$0$

Solución

Buscamos una expresión que nos permita representar al $0$, por ejemplo

$0=5-5$

$3+3+3$

Solución

Para resolver este ejercicio debemos notar que la expresión representa al $9$. Por lo tanto, buscamos una forma equivalente

$3+3+3=10-1$

$7X$

Solución

Buscamos una forma de representar $7X$, por ejemplo

$7x=4x+2x+x$

$13X−3$

Solución

Buscamos una forma equivalente de representar al $13X$ y al $-3$, por ejemplo

$13x-3=15x-2x-2-1$

$1.5X+8+6.5X$

Solución

Observemos que la expresión representa al $8X+8$, por lo tanto, buscamos una forma alternativa para representar cada término

$1.5x+8+6.5x=10x-2x+5+3$

$18X$

$2+9X$

Solución

Las expresiones no son equivalentes. Basta darnos cuenta que una representa al $18X$ y la otra $9X$

$20X$

$2\times10X$

Solución

Las expresiones son equivalentes, ambas representan la expresión $20X$

$3+3+3+3$

$3\times4$

Solución

Las expresiones son equivalentes, ambas representan al número $12$.

$15X−30$

$45-15-5X+15X$

Solución

Las expresiones no son equivalentes. En la primera hay $15X$ y en la segunda solo $10X$

$0.5X\times1$

$0.5X+0$

Solución

Las expresiones son equivalentes.

Si te interesa este artículo, también te pueden interesar los siguientes artículos:

• Incógnitas y expresiones algebraicas
• El valor numérico en expresiones algebraicas
• Multiplicación de expresiones algebraicas
• Simplificación de elementos / Simplificación de elementos semejantes

En la página web de Tutorela encontrarás una amplia gama de temas en matemáticas.

¿Qué es una expresión algebraica y ejemplos?

Una expresión algebraica es una combinación de números y letras (que representan números desconocidos) por medio de operaciones aritméticas.

¿Que son las expresiones algebraicas equivalentes?

Son expresiones algebraicas que tienen distinta estructura pero que representan la misma cantidad.

¿Cómo encontrar expresiones equivalentes?

Se busca modificar la estructura de la expresión de modo que no se altere la cantidad que representa.

Es importante que aprendamos a escribir expresiones algebraicas equivalentes en su forma más simple, ya que esto nos será muy útil al momento de resolver ecuaciones.

Simplificar $2x+5x+x$

Solución:

Para encontrar una expresión equivalente sumamos los coeficientes de cada término.

$\left(2+5+1\right)x=8x$

Reducir la expresión $8m+8-6m+3$

Solución:

Separamos los términos que tienen $m$ de los que no tienen y realizamos las operaciones indicadas

$8m+8-6m+3=8m-6m+8+3=(8-6)m+11=2m+11$

Encontrar una forma equivalente más simple para la expresión $8x+2y-3z+3y-4x+3z$

Solución:

Primero agrupamos los términos que tienen la misma letra, y después realizamos las operaciones indicadas

$8x+2y-3z+3y-4x+3z=8x-4x+2y+3y-3z+3z=(8-4)x+\left(2+3\right)y+\left(-3+3\right)z=4x+5y+0z=4x+5y$

Simplifica la expresión $6x+1-2x+3$, y posteriormente sustituye el valor $x=3$ en ambas expresiones y verifica que obtengas el mismo valor numérico.

Solución:

Primero simplificamos la expresión

$6x+1-2x+3=6x-2x+1+3=4x+4$

Ahora sustituimos $x=3$ en ambas expresiones

$6\left(3\right)+1-2\left(3\right)+3=18+1-6+3=18+1+3-6=22-6=16$

$4\left(3\right)+4=12+4=16$

En efecto, obtenemos el mismo valor numérico con ambas expresiones.

Resuelve la ecuación $5x+2+3x+7-2x-5=16$

Solución:

Antes de despejar la incógnita, encontraremos una expresión equivalente del primer miembro

$5x+2+3x+7-2x-5=16$

$5x+3x-2x+2+7-5=16$

$\left(5+3-2\right)x+4=16$

$6x+4=16$

Ahora si, despejamos la incógnita

$6x=16-4$

$6x=12$

$x=\frac{12}{6}$

$x=2$