Realizaremos la misma operación de multiplicación en el numerador y el denominador: se conservará el valor de la fracción.
Puedes amplificar tantas veces como quieras y en cualquier número.
Ejercicios de Simplificación y Amplificación de Fracciones
Practica simplificar y amplificar fracciones simples con ejercicios paso a paso. Aprende a reducir fracciones y encontrar fracciones equivalentes fácilmente.
📚Domina la Simplificación y Amplificación de Fracciones
- Simplificar fracciones dividiendo numerador y denominador por el mismo número
- Amplificar fracciones multiplicando numerador y denominador por el mismo valor
- Identificar el máximo común divisor para simplificar al máximo
- Encontrar fracciones equivalentes usando amplificación
- Completar ejercicios con números faltantes en fracciones equivalentes
- Reconocer cuándo una fracción ya está en su forma más simple
Entendiendo la Simplificación y amplificación de fracciones simples
Explicación completa con ejemplos
Simplificación y amplificación de fracciones simples
Para amplificar fracciones
Para simplificar fracciones:
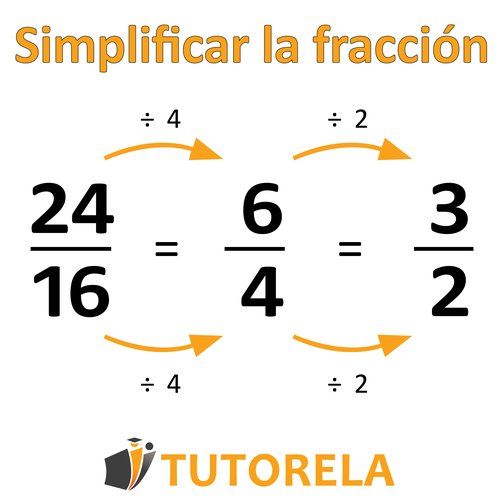
Realizaremos la misma operación de división en el numerador y el denominador: se conservará el valor de la fracción.
Esto solo se puede hacer con un número que sea completamente divisible por el numerador y el denominador.
Es posible simplificar solo hasta llegar a una fracción en la que no es posible encontrar un número que divida sin resto tanto en el numerador como en el denominador.
Practicar Simplificación y amplificación de fracciones simples
Pon a prueba tus conocimientos con más de 17 cuestionarios
Simplifica la siguiente fracción por el factor 6 y marca su valor después de la simplificación.
\( \frac{36}{18}= \)
ejemplos con soluciones para Simplificación y amplificación de fracciones simples
Soluciones paso a paso incluidas
Ejercicio #1
Simplifica la siguiente fracción por el factor 1 y elija su valor apropiado después de la simplificación:
Solución Paso a Paso
Simplificamos de la siguiente manera, dividiendo el numerador por 1 y el denominador por 1:
Respuesta:
Solución en video
Ejercicio #2
Simplifica la siguiente fracción por el factor 2 y elija su valor apropiado después de la simplificación:
Solución Paso a Paso
Simplificamos de la siguiente manera, dividimos tanto el numerador como el denominador por 2:
Respuesta:
Solución en video
Ejercicio #3
Simplifica la siguiente fracción por el factor 4 y elija su valor apropiado después de la simplificación:
Solución Paso a Paso
Simplificamos de la siguiente manera, dividimos tanto el numerador como el denominador por 4:
Respuesta:
Solución en video
Ejercicio #4
Simplifica la siguiente fracción por el factor 4 y elija su valor apropiado después de la simplificación:
Solución Paso a Paso
Simplificamos de la siguiente manera, dividiendo el numerador por 4 y el denominador por 4:
Respuesta:
Solución en video
Ejercicio #5
Simplifica la siguiente fracción por el factor 3 y elija su valor apropiado después de la simplificación:
Solución Paso a Paso
Simplificamos de la siguiente manera, dividiendo el numerador por 3 y el denominador por 3:
Respuesta:
Solución en video
Preguntas Frecuentes
¿Cómo simplificar una fracción paso a paso?
+Para simplificar una fracción: 1) Encuentra un número que divida exactamente tanto el numerador como el denominador, 2) Divide ambos por ese número, 3) Repite hasta que no encuentres más divisores comunes. Por ejemplo: 24/16 ÷ 8 = 3/2.
¿Qué significa amplificar una fracción?
+Amplificar una fracción significa multiplicar tanto el numerador como el denominador por el mismo número. Esto crea una fracción equivalente con números más grandes pero el mismo valor. Por ejemplo: 1/2 × 4 = 4/8.
¿Cuándo no se puede simplificar más una fracción?
+Una fracción no se puede simplificar más cuando el numerador y denominador no tienen divisores comunes excepto el 1. Por ejemplo, 3/5 ya está en su forma más simple porque 3 y 5 no comparten divisores comunes.
¿Por qué el valor de la fracción no cambia al simplificar o amplificar?
+El valor no cambia porque realizas la misma operación (multiplicación o división) en ambas partes de la fracción. Es como tener media pizza: ya sea 1/2 o 4/8, sigues teniendo la misma cantidad de pizza.
¿Cómo encontrar el número que falta en fracciones equivalentes?
+Observa qué operación se hizo en la parte conocida (numerador o denominador), luego aplica la misma operación a la parte desconocida. Si 2/8 = 4/□, como 2×2=4, entonces 8×2=16.
¿Cuál es la diferencia entre simplificar y amplificar fracciones?
+Simplificar usa división para hacer los números más pequeños (6/12 ÷ 6 = 1/2), mientras que amplificar usa multiplicación para hacer los números más grandes (1/2 × 4 = 4/8). Ambas mantienen el mismo valor.
¿Qué es el máximo común divisor en fracciones?
+Es el número más grande que divide exactamente tanto el numerador como el denominador. Usar el MCD permite simplificar la fracción de una sola vez hasta su forma más simple.
¿Se pueden amplificar las fracciones por cualquier número?
+Sí, puedes amplificar una fracción por cualquier número positivo tantas veces como quieras. El valor de la fracción permanecerá igual siempre que multipliques tanto el numerador como el denominador por el mismo número.