Realizaremos la misma operación de multiplicación en el numerador y el denominador: se conservará el valor de la fracción.
Puedes amplificar tantas veces como quieras y en cualquier número.
Realizaremos la misma operación de multiplicación en el numerador y el denominador: se conservará el valor de la fracción.
Puedes amplificar tantas veces como quieras y en cualquier número.
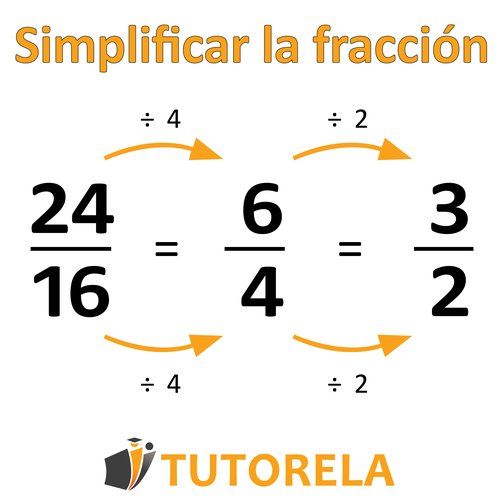
Realizaremos la misma operación de división en el numerador y el denominador: se conservará el valor de la fracción.
Esto solo se puede hacer con un número que sea completamente divisible por el numerador y el denominador.
Es posible simplificar solo hasta llegar a una fracción en la que no es posible encontrar un número que divida sin resto tanto en el numerador como en el denominador.
AmplÍa la siguiente fracción por el factor 10:
\( \frac{1}{16}= \)
Simplifica y amplificar fracciones es un tema fácil y agradable que te acompañará en casi todos los ejercicios con fracciones.
Simplificar y amplificar una fracción es en realidad una operación de multiplicación o división que se realiza en la fracción para que el valor real de la fracción no cambie y simplemente se vea diferente.
Amplificación: una operación de multiplicación (que se realiza tanto en el numerador como en el denominador).
Simplificación: una operación de división (que se realiza tanto en el numerador como en el denominador).
Piense en una pizza con porciones: una pizza familiar normal que se vende en las pizzerías.
Se comunica para realizar el pedido y le solicita al vendedor, ponga aceitunas en la mitad de la pizza.

Recibirás pizza con aceitunas.
Pero, ¿qué pasaría si le dijeras al vendedor, por favor, pon aceitunas en triángulos de la pizza?
Veamos:
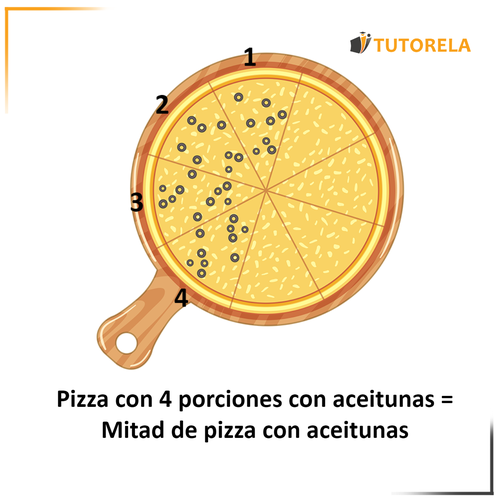
Incluso entonces obtendrías media pizza con aceitunas.
Es decir que: -> cuatro porciones de es igual a
Ahora veamos esto en el ejercicio
Amplificamos la fracción por
Solución:
Multiplicamos por tanto en el numerador como el denominador y obtenemos:
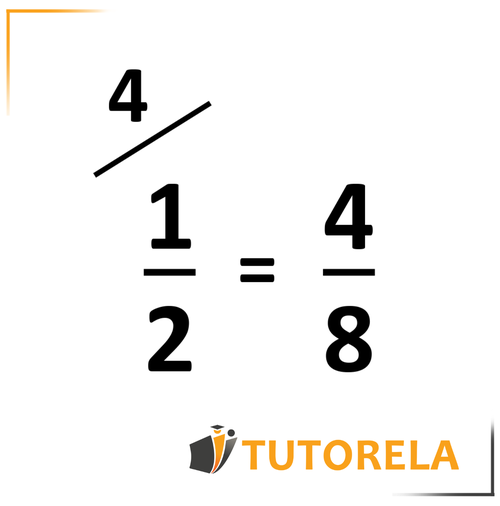
Tenga en cuenta el signo que generalmente se usa para amplificar.
Si multiplicamos tanto el numerador como el denominador por el mismo número, el valor de la fracción no cambiará y las fracciones serán iguales, exactamente como en la pizza.
Nota importante: ¡podemos amplificar la fracción tantas veces como queramos y por cualquier número que queramos y aún así el valor no cambiará!
Por ejemplo, incluso si en lugar de amplificarse por ampliaríamos por , obtendríamos:
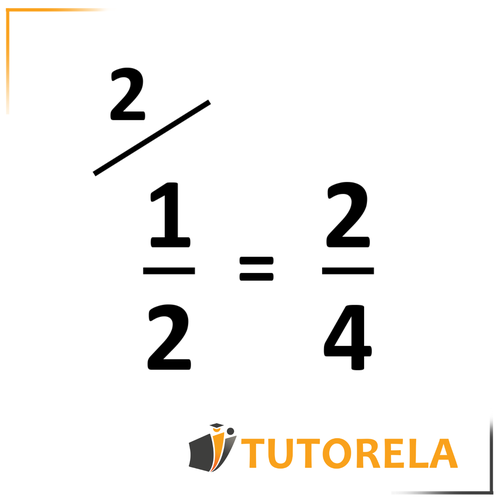
que también es igual a
Completa el número que falta
Solución:
Vemos que en el numerador se convierte en . Es decir, es multiplicado por. Por lo tanto, también multiplicamos el denominador por el número para alcanzar el resultado correcto.
Después de todo, aprendimos que las fracciones serán iguales solo si realizamos la operación tanto en el numerador como en el denominador.
Obtenemos:
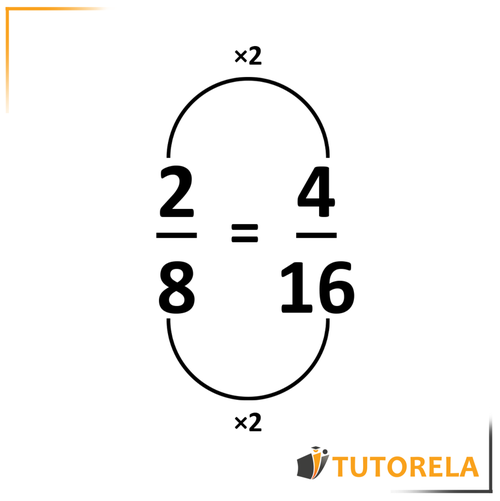
AmplÍa la siguiente fracción por el factor 2:
\( \frac{10}{12}= \)
AmplÍa la siguiente fracción por el factor 3:
\( \frac{6}{10}= \)
AmplÍa la siguiente fracción por el factor 5:
\( \frac{3}{10}= \)
La simplificación de fracciones es una operación de división que se realiza tanto en el numerador como en el denominador y conserva el valor de la fracción.
Es posible simplificar solo por un número que es divisible sin resto tanto en el numerador como en el denominador.
¿Cuándo no podemos simplificar una fracción?
Cuando el numerador y el denominador no son completamente divisibles por el mismo número.
Simplificar la fracción por .
Solución:
Dividimos el numerador y el denominador por y obtenemos:
Sección extra:
Simplificamos la fracción por el número que elijan (excepto por )
Solución:
Debemos elegir un número que divida el numerador y el denominador sin resto.
Se nos pregunta: ¿por qué número puedes dividir y ?
La respuesta puede ser: o . Por ejemplo
Elegimos: y simplificamos:
Simplificamos la fracción:
Solución:
Este ejercicio no tiene solución. Esta fracción no se puede simplificar más puesto que no hay número que sea divisible por y también por sin resto.
Complete el número faltante
Solución:
Vemos que en el numerador se convierte en . Es decir se divide por . Por lo tanto, dividimos también en el denominador por el número para para llegar al resultado correcto ya que aprendimos que las fracciones serán iguales solo si realizamos la operación tanto en el numerador como en el denominador.
Obtenemos:
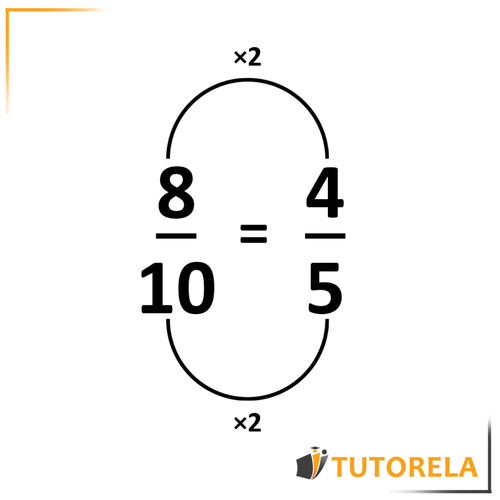
Nota: ¡la amplificación no significa que la fracción se hace más grande y la simplificación no significa que la fracción se hace más pequeña!
Simplifica la siguiente fracción por el factor 1 y elija su valor apropiado después de la simplificación:
Simplificamos de la siguiente manera, dividiendo el numerador por 1 y el denominador por 1:
Simplifica la siguiente fracción por el factor 3 y elija su valor apropiado después de la simplificación:
Simplificamos de la siguiente manera, dividiendo el numerador por 3 y el denominador por 3:
Simplifica la siguiente fracción por un factor de 5 y elige su valor apropiado después de la simplificación:
Simplificamos de la siguiente manera, dividimos tanto el numerador como el denominador por 5:
Simplifica la siguiente fracción por el factor 2 y elija su valor apropiado después de la simplificación:
Simplifiquemos de la siguiente manera, dividimos tanto el numerador como el denominador por 2:
Simplifica la siguiente fracción por el factor 4 y elija su valor apropiado después de la simplificación:
Simplificamos de la siguiente manera, dividimos tanto el numerador como el denominador por 4:
AmplÍa la siguiente fracción por el factor 3:
\( \frac{2}{15}= \)
Simplifica la siguiente fracción por el factor 1 y elija su valor apropiado después de la simplificación:
\( \frac{3}{10}= \)
Simplifica la siguiente fracción por el factor 3 y elija su valor apropiado después de la simplificación:
\( \frac{3}{6}= \)