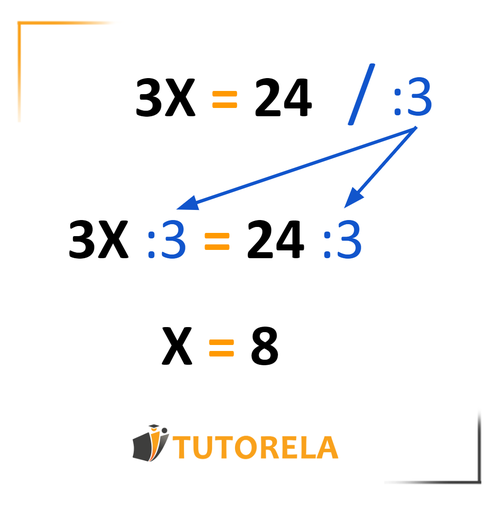
Con este método podemos multiplicar o dividir a la vez ambos miembros de la ecuación por un mismo elemento sin alterar por tanto el valor general de la ecuación. Esto quiere decir que el resultado final de la ecuación no se verá afectado porque hayamos multiplicado o dividido ambos miembros por un mismo elemento o número.