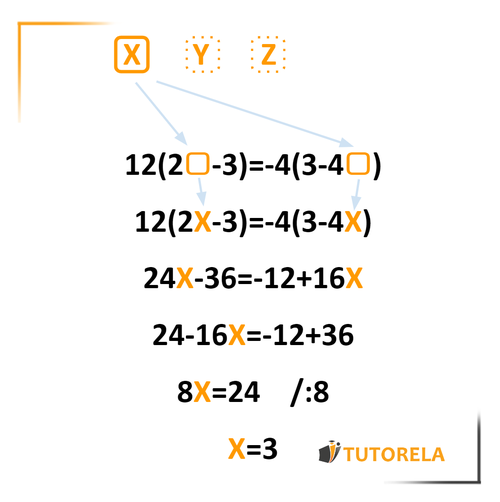
Las ecuaciones son expresiones algebraicas que contienen números e incógnitas. Es importante saber diferenciar estos dos grupos: los números son valores fijos mientras que las incógnitas, como su nombre lo indica, representan valores desconocidos (al menos al principio), y en la mayoría de los casos se nos pide que encontremos cual es este valor.
Por ejemplo: