Ejercicios de Ecuaciones Lineales con Una Variable - Práctica

Resuelve ecuaciones de primer grado con una incógnita paso a paso. Aprende a despejar variables usando suma, resta, multiplicación y división con ejercicios prácticos.

📚Domina las Ecuaciones Lineales con Ejercicios Paso a Paso

Resolver ecuaciones simples usando suma y resta para aislar la variable
Aplicar multiplicación y división para despejar incógnitas con coeficientes
Trabajar con ecuaciones que contienen fracciones y términos mixtos
Verificar soluciones sustituyendo valores en la ecuación original
Identificar los miembros izquierdo y derecho de una ecuación correctamente
Resolver ecuaciones de la forma ax + b = c usando múltiples operaciones

Entendiendo la Ecuaciones de primer grado con una incógnita

Explicación completa con ejemplos

La solución de una ecuación es, de hecho, un valor numérico que, si lo colocamos en lugar de la incógnita (o la variable), lograremos igualdad entre los dos miembros de la ecuación, o sea, obtendremos un «enunciado verdadero». En ecuaciones de primer grado con una incógnita, sólo puede haber una solución.

Ejemplo:

$X - 1 = 5$

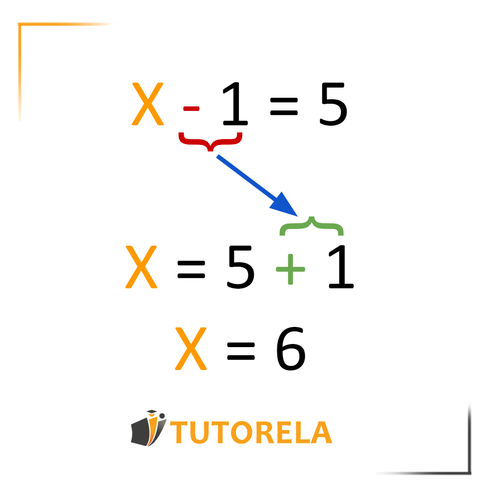
Ésta es una ecuación con una incógnita o variable indicada con la letra $X$ . La ecuación está compuesta por dos miembros separados mediante el uso del signo igual $=$ . El miembro izquierdo es todo lo que se encuentra a la izquierda del signo $=$ , y el miembro derecho es todo lo que está a la derecha de dicho signo.

Nuestro objetivo es aislar la variable (o despejar la variable) $X$ de modo tal que sólo ella quede en uno de los miembros de la ecuación. Así descubriremos su valor. En este artículo aprenderemos a utilizar las cuatro operaciones matemáticas (suma, resta, multiplicación y división) para aislar la variable \( X \.

Explicación completa

Practicar Ecuaciones de primer grado con una incógnita

Pon a prueba tus conocimientos con más de 42 cuestionarios

Resuelve la ecuación

$5x \cdot 3 = 45$

ejemplos con soluciones para Ecuaciones de primer grado con una incógnita

Soluciones paso a paso incluidas

Ejercicio #1

Resuelve para X:

$x - 3 + 5 = 8 - 2$

Solución Paso a Paso

Primero, simplifica ambos lados de la ecuación:

Lado izquierdo: $x - 3 + 5 = x + 2$

Lado derecho: $8 - 2 = 6$

Ahora la ecuación es: $x + 2 = 6$

Resta 2 de ambos lados para aislar $x$ :

$x + 2 - 2 = 6 - 2$

Simplificando se obtiene:

$x = 4$

Respuesta:

Solución en video

Ejercicio #2

Resuelve para X:

$9 - x = 16 - 7$

Solución Paso a Paso

Primero, simplifica el lado derecho de la ecuación:
$16 - 7 = 9$
Por lo tanto, la ecuación se convierte en $9 - x = 9$ .
Como ambos lados son iguales, $x$ debe ser $0$ .
Por lo tanto, la solución es $x = 0$ .

Respuesta:

Solución en video

Ejercicio #3

Resuelve para X:

$5 + x - 3 = 2 + 1$

Solución Paso a Paso

Para resolver $5 + x - 3 = 2 + 1$ , primero simplificamos ambos lados:

Lado izquierdo:
$5 - 3 + x = 2 + x$

Lado derecho:
$2 + 1 = 3$

Ahora la ecuación es $2 + x = 3$ .

Resta 2 en ambos lados:
$x = 3 - 2$

Por lo tanto, $x = 1$ .

Respuesta:

Solución en video

Ejercicio #4

Resuelve para X:

$3 + x - 2 = 7 - 3$

Solución Paso a Paso

Primero, simplifica ambos lados de la ecuación:

Lado izquierdo: $3 + x - 2 = 1 + x$

Lado derecho: $7 - 3 = 4$

Entonces la ecuación se convierte en:

$1 + x = 4$

Después, aísla $x$ restando 1 en ambos lados:

$1 + x - 1 = 4 - 1$

Esto se simplifica a:

$x = 3$

Respuesta:

Solución en video

Ejercicio #5

Resuelve para X:

$x + 4 - 2 = 6 + 1$

Solución Paso a Paso

Primero, simplifica ambos lados de la ecuación:

Lado izquierdo: $x + 4 - 2 = x + 2$

Lado derecho: $6 + 1 = 7$

Ahora la ecuación es: $x + 2 = 7$

Resta 2 en ambos lados para aislar $x$ :

$x + 2 - 2 = 7 - 2$

Simplificando se obtiene:

$x = 5$

Respuesta:

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Ecuaciones de primer grado con una incógnita

¿Cómo resolver una ecuación lineal con una variable paso a paso?

Para resolver una ecuación lineal: 1) Identifica la variable a despejar, 2) Aplica operaciones inversas a ambos lados para aislar la variable, 3) Simplifica los cálculos, 4) Verifica la solución sustituyendo el valor en la ecuación original.

¿Qué operaciones matemáticas se usan para despejar una incógnita?

Las cuatro operaciones básicas: suma, resta, multiplicación y división. La clave es aplicar la operación inversa - si hay suma, restas; si hay multiplicación por 2, divides por 2 en ambos lados de la ecuación.

¿Cómo verificar si la solución de una ecuación es correcta?

Sustituye el valor encontrado en lugar de la variable en la ecuación original. Si obtienes el mismo número en ambos lados del signo igual, la solución es correcta. Por ejemplo: Si x=6 y la ecuación es x-1=5, entonces 6-1=5, que es verdadero.

¿Qué hacer cuando hay fracciones en una ecuación lineal?

Multiplica ambos lados de la ecuación por el denominador para eliminar la fracción. Por ejemplo, en (1/3)x = 5, multiplicas ambos lados por 3 para obtener x = 15.

¿Cuáles son los errores más comunes al resolver ecuaciones lineales?

Los errores principales incluyen: • No aplicar la misma operación a ambos lados • Confundir operaciones inversas • Errores de cálculo aritmético • No verificar la solución final • Olvidar el signo negativo en coeficientes

¿Qué significa que una ecuación tenga una sola solución?

Las ecuaciones lineales con una variable tienen exactamente una solución porque solo existe un valor que hace verdadera la igualdad. Este valor único es el que buscamos al despejar la variable.

¿Cómo resolver ecuaciones del tipo 2x + 3 = 5?

Sigue estos pasos: 1) Resta 3 de ambos lados: 2x = 2, 2) Divide ambos lados por 2: x = 1, 3) Verifica: 2(1) + 3 = 5 ✓

¿Qué diferencia hay entre miembro izquierdo y derecho de una ecuación?

El miembro izquierdo es todo lo que está a la izquierda del signo igual (=), y el miembro derecho es todo lo que está a la derecha. Ambos deben tener el mismo valor para que la ecuación sea verdadera.

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Más Recursos y Enlaces

Explora más recursos y enlaces relacionados con Ecuaciones de primer grado con una incógnita

Practicar Ecuaciones de primer grado con una incógnita Practicar Resolución de ecuaciones utilizando la propiedad distributiva Practicar Resolución de ecuaciones sumando o restando un mismo número de ambos miembros Practicar Resolución de ecuaciones multiplicando o dividiendo ambos miembros por un mismo número Practicar Resolución de ecuaciones mediante la simplificación de elementos iguales