Principios y métodos para resolver ecuaciones de primer grado con una incógnita
Si este artículo te interesó también te pueden interesar los siguientes artículos:
En la página web de Tutorela encontrarás una gran variedad de artículos sobre matemáticas
Ejemplos y ejercicios
Ejercicio 1
Resuelve la siguiente ecuación:
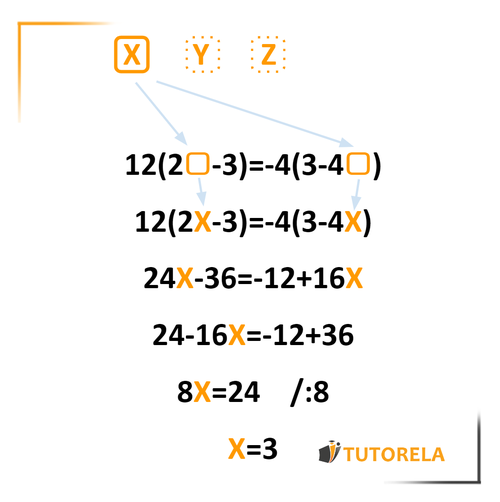
12(2X−3)=−4(3−4X)
Solución:
Para resolver la ecuación, primero hacemos los productos de los dos lados de la ecuación:
24X−36=−12+16X
A continuación agruparemos los términos semejantes, de modo que del lado izquierdo de la ecuación aparezcan todas las incógnitas, mientras que del lado derecho de la ecuación aparezcan los números. Recuerda, que al transponer los términos de un lado a otro de la ecuación, cambiará su signo. Es decir, que si está sumando, pasará hacia el otro lado restando, y viceversa.
24X−16X=−12+36
Luego reducimos los términos semejantes:
8X=24
Ahora, para encontrar el valor de la incógnita, dividimos ambos lados de la ecuación entre 8 y obtendremos:
8X/8=24/8
X=3
Así, X=3 es la solución de la ecuación.
Respuesta:
X=3
¡Únete a 30,000 estudiantes destacados en matemáticas!
Práctica ilimitada, guía de expertos: mejora tus habilidades matemáticas hoy
Comprueba tu conocimiento
Ejercicio 2
Resuelve la siguiente ecuación:
8(2−5X)−12(1−X)=0
Para resolver esta ecuación, primero hacemos el producto del lado izquierdo de la ecuación, obteniendo:
16−40X−12+12X=0
A continuación agrupamos los términos semejantes, de modo que del lado izquierdo de la ecuación aparezcan todas las incógnitas, mientras que del lado derecho de la ecuación aparecerán los números. Recuerda, que al transponer los términos de un lado a otro de la ecuación, cambiará su signo.
−40X+12X=12−16
El siguiente paso será reducir los términos semejantes:
−28X=−4
Ahora, para encontrar el valor de la incógnita, dividimos los dos lados de la ecuación entre (-28) y obtendremos:
−28X/−28=−4/−28
Y por último reducimos la fracción:
X=284=71
Respuesta:
X=71
Ejercicio 3
Resuelve la siguiente ecuación:
−6(−X−1)+10(2−X)=16
Para resolver la ecuación, primero hacemos los productos de los dos lados de la ecuación:
6X+6+20−10X=16
A continuación agrupamos los términos semejantes, de modo que del lado izquierdo de la ecuación aparezcan todas las incógnitas, mientras que del lado derecho de la ecuación aparecen los números. Recuerda, que al transponer los términos de un lado a otro de la ecuación, cambiará su signo. Es decir, que si está sumando, pasará hacia el otro lado restando, y viceversa.
6X−10X=16−6−20
El siguiente paso será reducir los términos semejantes:
−4X=−10
Ahora, para encontrar el valor de la incógnita, dividimos ambos lados de la ecuación entre (-4), y obtendremos:
−4X/−4=−−410
X=410=2.5
Respuesta:
X=2.5
¿Sabes cuál es la respuesta?
Ejercicio 4
Resuelve la siguiente ecuación:
321⋅y=21
Solución
Notemos que:
321=27
Así la ecuación es equivalente a:
27⋅y=21
Ahora, dividimos por 7/2 ambos lados de la ecuación y obtenemos:
y=2721=6
y=6
Respuesta
y=6
Ejercicio 5
Resuelve la siguiente ecuación:
431⋅x=2132
Solución
Notemos que:
431=313
y
2132=365
Así, la ecuación es equivalente a:
313⋅x=365
Dividir ambos lados de la ecuación por:
313
para simplificar
x=313365
x=5
Respuesta
x=5
Comprueba que lo has entendido
Ejercicio 6
Resuelve la siguiente ecuación:
3x+4+x+1=9
Solución
A continuación agrupamos los términos semejantes, de modo que del lado izquierdo de la ecuación aparezcan todas las incógnitas, mientras que del lado derecho de la ecuación aparecen los números.
3x+x=9−4−1
Sumamos los términos semejantes:
4x=4
Dividimos ambos lados de la ecuación por 4
4x/4=4/4
Respuesta
x=1
Ejercicio 8
Resuelve la siguiente problema:
¿Cuál es el dominio de aplicación de la ecuación?
2(3+y)+4xyz=8
Solución
Debemos calcular cuándo el denominador del lado derecho de la ecuación es igual a cero, es decir:
2(3+y)+4=0
Multiplicamos por 2 en los dos elementos de los paréntesis
6+2y+4=0
Sumamos en consecuencia
10+2y=0
Pasamos a 10 a la sección de la derecha
2y=−10
Dividimos por 2
y=−5
y=−5
Si Y es igual a menos 5 entonces el denominador es igual a 0 y el ejercicio no tiene solución
Respuesta
y=−5
¿Crees que podrás resolverlo?
Preguntas sobre el tema
¿Qué es una ecuación de primer grado con una incógnita?
Es una expresión matemática que consiste de una incógnita o variable y números en la cual se debe hallar el valor de variable que generalmente es denotada por X.
Ejemplos
a) 3x−5=2x+4.
b) 4−x=10.
c) 4(x−4)+2=2x.
¿Cómo resolver ecuaciones de primer grado con una incógnita?
Aislando la incógnita, es decir, dejarla sola en algún lado de la igualdad.
Comprueba tu conocimiento
¿Qué son las ecuaciones de primer grado con dos incógnitas?
Es una expresión matemática que consiste de dos incógnita o variables y números en la cual se debe hallar el valor de las variables que generalmente son denotados por X y Y.
¿Cómo despejar una incógnita?
Aislando la variable o incógnita utilizando operaciones como la suma, resta, multiplicación y división.
¿Sabes cuál es la respuesta?
ejemplos con soluciones para Ecuaciones de primer grado con una incógnita
Ejercicio #1
Resuelve para X:
x−3+5=8−2
Solución en video
Solución Paso a Paso
Primero, simplifica ambos lados de la ecuación:
Lado izquierdo: x−3+5=x+2
Lado derecho: 8−2=6
Ahora la ecuación es: x+2=6
Resta 2 de ambos lados para aislar x:
x+2−2=6−2
Simplificando se obtiene:
x=4
Respuesta
Ejercicio #2
Resuelve para X:
9−x=16−7
Solución en video
Solución Paso a Paso
Primero, simplifica el lado derecho de la ecuación:
16−7=9
Por lo tanto, la ecuación se convierte en 9−x=9.
Como ambos lados son iguales, x debe ser 0.
Por lo tanto, la solución es x=0.
Respuesta
Ejercicio #3
Resuelve para X:
5+x−3=2+1
Solución en video
Solución Paso a Paso
Para resolver 5+x−3=2+1, primero simplificamos ambos lados:
Lado izquierdo:
5−3+x=2+x
Lado derecho:
2+1=3
Ahora la ecuación es 2+x=3.
Resta 2 en ambos lados:
x=3−2
Por lo tanto, x=1.
Respuesta
Ejercicio #4
Resuelve para X:
3+x−2=7−3
Solución en video
Solución Paso a Paso
Primero, simplifica ambos lados de la ecuación:
Lado izquierdo: 3+x−2=1+x
Lado derecho: 7−3=4
Entonces la ecuación se convierte en:
1+x=4
Después, aísla x restando 1 en ambos lados:
1+x−1=4−1
Esto se simplifica a:
x=3
Respuesta
Ejercicio #5
Resuelve para X:
x+4−2=6+1
Solución en video
Solución Paso a Paso
Primero, simplifica ambos lados de la ecuación:
Lado izquierdo: x+4−2=x+2
Lado derecho: 6+1=7
Ahora la ecuación es: x+2=7
Resta 2 en ambos lados para aislarx:
x+2−2=7−2
Simplificando se obtiene:
x=5
Respuesta