En este artículo conoceremos las ecuaciones y aprenderemos caminos simples para resolverlas.
Ahora veremos ecuaciones con una sola incógnita
Por ejemplo
Volvamos a la ecuación del ejemplo anterior:
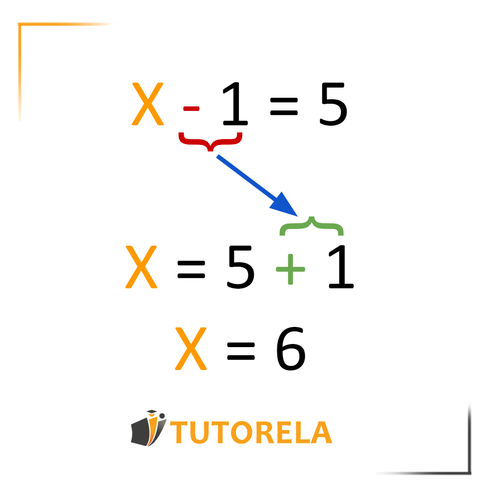
X−1=5
Queremos aislar la X. Para hacerlo sumaremos 1 a ambos miembros de la ecuación.
Lo escribiremos así:
X−1=5
Obtendremos:
x−1+1=5+1
Es decir:
X=6
Y, ésta es la solución para nuestra ecuación. Siempre podemos corroborar si lo hemos hecho bien colocando nuestra respuesta en la ecuación original. Pongamos X=6 en la ecuación
X−1=5
y obtendremos
6−1=5
5=5
éste es un enunciado verdadero, 5 realmente equivale a 5, es decir, nuestra solución es correcta.
¡Únete a 30,000 estudiantes destacados en matemáticas!
Práctica ilimitada, guía de expertos: mejora tus habilidades matemáticas hoy
Comprueba tu conocimiento
Otro ejemplo
Z+7=15
Primero veamos que esta vez la variable es Z. La variable se puede señalar con la letra que queramos.
Tal como lo hemos explicado antes, nos interesa encontrar el valor de la Z que nos otorgará la solución para la ecuación. Por lo tanto, ahora intentaremos aislar la Z. Lo haremos restando 7 de los dos miembros de la ecuación.
Se ve así:
Z+7=15
Obtendremos:
Z+7−7=15–7
Z=8
Ésta es la solución de la ecuación. Reiteramos, siempre es conveniente corroborar si lo hemos encontrado el valor correcto de la incógnita colocando nuestra respuesta en la ecuación original.
Recordemos cuál era la ecuación original:
Z+7=15
pongamos
Z=8
y obtendremos:
8+7=15
15=15
Éste realmente es un enunciado verdadero, es decir, la respuesta que recibimos es correcta.
Solución de ecuaciones aplicando operaciones de multiplicar y dividir
Hasta ahora hemos resuelto ecuaciones aplicando operaciones de suma y resta a ambos lados de la ecuación. Ahora veremos otros ejemplos de ecuaciones que solucionaremos con operaciones de multiplicar y dividir:
¿Sabes cuál es la respuesta?
Ejercicio 1
Encuentra el valor de la incógnita de la siguiente ecuación y corrobora que sea correcto.
2X=8
Queremos aislar la X. Dividimos ambos miembros de la ecuación por 2. Lo escribiremos así:
2X/2=8/2
y obtendremos:
X=4
También en este caso conviene colocar la solución en la ecuación original para ver si lo hemos hecho bien:
2×4=8
8=8
Obtuvimos un resultado correcto, o sea, nuestra solución está bien.
Ejercicio 2
Encuentra el valor de la incógnita de la siguiente ecuación y corrobora que sea correcto.
−3Y=18
Para aislar la variable Y dividimos ambos miembros de la ecuación por −3
−3Y/−3=18/−3
Y=−6
Para verificar nuestro resultado, siempre conviene colocarlo en la ecuación original. ¡Inténtalo!
Comprueba que lo has entendido
Ejercicio 3
Encuentra el valor de la incógnita de la siguiente ecuación y corrobora que sea correcto.
31x=5
Aquí tenemos una fracción en la ecuación. Queremos deshacernos de ella y aislar la X. Multiplicamos ambos miembros de la ecuación por 3
3×31x=3×5
Obtendremos:
x=15
Para verificarlo colocaremos el resultado obtenido en la ecuación original:
31×15=5
5=5
Es decir, el resultado obtenido es correcto.
Ejercicio 4
Encuentra el valor de la incógnita de la siguiente ecuación y corrobora que sea correcto.
2x+3=5
Este ejercicio requiere operaciones de restar y de dividir. Primeramente, restamos 3 de los dos miembros de la ecuación:
2x+3=5
2x+3−3=5–3
2x=2
Ahora dividiremos los dos miembros de la ecuación por 2 y obtendremos:
2x/2=2/2
X=1
Coloquemos el resultado obtenido en la ecuación original para controlar si lo hemos hecho bien:
2×1+3=5
5=5
Es decir, el resultado obtenido es correcto.
¿Crees que podrás resolverlo?
Ejercicio 5
Encuentra el valor de la incógnita de la siguiente ecuación y corrobora que sea correcto.
X−6=0
Este ejercicio requiere la operación de sumar 6 en ambos miembros de la ecuación, por lo que tenemos:
X−6+6=0+6
Simplificando obtenemos que la solución de la ecuación es X=6 ya que si ponemos 6 en lugar de la X obtendremos el resultado 0 en ambos lados de la ecuación, tendremos dos miembros equivalentes.
Ejercicio 6
Encuentra el valor de la incógnita de la siguiente ecuación y corrobora que sea correcto.
2X−6=0
Este ejercicio requiere la operación de sumar 6 en ambos miembros de la ecuación, por lo que tenemos:
2X−6+6=0+6
2X=6
Ahora dividimos por 2 ambos lados de la ecuación :
2X/2=6/2
X=3
La solución de la ecuación es X=3 ya que si ponemos 3 en lugar de la X obtendremos el resultado 0 en ambos lados de la ecuación, tendremos dos miembros equivalentes.
Comprueba tu conocimiento
Ejercicio 7
Encuentra el valor de la incógnita de la siguiente ecuación y corrobora que sea correcto.
3X−5=16
Este ejercicio requiere la operación de sumar 5 en ambos miembros de la ecuación, por lo que tenemos:
3X−5+5=16+5
3X=21
Ahora dividimos por 3 ambos lados de la ecuación:
3X/3=21/3
X=7
La solución de la ecuación es X=7 ya que si ponemos 7 en lugar de la X obtendremos el resultado 16 en ambos lados de la ecuación, tendremos dos miembros equivalentes.
Preguntas sobre el tema
¿Cómo despejar una incógnita?
Aislando a la variable con operaciones matemáticas.
¿Sabes cuál es la respuesta?
¿Cómo aislar una variable o incógnita?
Pasando términos semejantes a cada lado de la igualdad y haciendo operaciones matemáticas.
¿Cómo corroborar la solución de una ecuación?
Sustituyendo el valor encontrado en la ecuación original y comprobar que se cumple la igualdad.
Comprueba que lo has entendido
¿Qué es una incógnita?
Es el valor desconocido de la ecuación.
¿Cómo resolver una ecuación de primer orden con una incógnita?
Aislando a la variable con operaciones matemáticas.
¿Crees que podrás resolverlo?
¿Qué es una ecuación de primer orden con una incógnita?
Es una igualdad matemática que involucra una variable elevada a la primer potencia y valores fijos que son los números.
Si este artículo te interesó también te pueden interesar los siguientes artículos:
En la página web de Tutorela encontrarás una gran variedad de artículos sobre matemáticas
Comprueba tu conocimiento
ejemplos con soluciones para Ecuaciones de primer grado con una incógnita
Ejercicio #1
Resuelve para X:
x−3+5=8−2
Solución en video
Solución Paso a Paso
Primero, simplifica ambos lados de la ecuación:
Lado izquierdo: x−3+5=x+2
Lado derecho: 8−2=6
Ahora la ecuación es: x+2=6
Resta 2 de ambos lados para aislar x:
x+2−2=6−2
Simplificando se obtiene:
x=4
Respuesta
Ejercicio #2
Resuelve para X:
9−x=16−7
Solución en video
Solución Paso a Paso
Primero, simplifica el lado derecho de la ecuación:
16−7=9
Por lo tanto, la ecuación se convierte en 9−x=9.
Como ambos lados son iguales, x debe ser 0.
Por lo tanto, la solución es x=0.
Respuesta
Ejercicio #3
Resuelve para X:
5+x−3=2+1
Solución en video
Solución Paso a Paso
Para resolver 5+x−3=2+1, primero simplificamos ambos lados:
Lado izquierdo:
5−3+x=2+x
Lado derecho:
2+1=3
Ahora la ecuación es 2+x=3.
Resta 2 en ambos lados:
x=3−2
Por lo tanto, x=1.
Respuesta
Ejercicio #4
Resuelve para X:
3+x−2=7−3
Solución en video
Solución Paso a Paso
Primero, simplifica ambos lados de la ecuación:
Lado izquierdo: 3+x−2=1+x
Lado derecho: 7−3=4
Entonces la ecuación se convierte en:
1+x=4
Después, aísla x restando 1 en ambos lados:
1+x−1=4−1
Esto se simplifica a:
x=3
Respuesta
Ejercicio #5
Resuelve para X:
x+4−2=6+1
Solución en video
Solución Paso a Paso
Primero, simplifica ambos lados de la ecuación:
Lado izquierdo: x+4−2=x+2
Lado derecho: 6+1=7
Ahora la ecuación es: x+2=7
Resta 2 en ambos lados para aislarx:
x+2−2=7−2
Simplificando se obtiene:
x=5
Respuesta