Podemos añadir ángulos y obtener el resultado de su suma y también restarlos y obtener la diferencia entre ellos.
Aún si los ángulos no tienen ningún número aprenderemos cómo representar su suma o resta y llegar al resultado correcto.
Suma y diferencia de ángulos
Suma y diferencia de ángulos
Suma de ángulos
Para encontrar la suma de ángulos éstos tienen que tener un vértice en común.
Diferencia entre ángulos
Del mismo modo que hemos sumado los ángulos también podremos restar uno de otro.
¡Pruébate en suma y diferencia de angulos!
Indica qué ángulo es mayor
Aún si los ángulos no tienen ningún número aprenderemos cómo representar su suma o resta y llegar al resultado correcto: el nombramiento correcto del ángulo que recibimos como resultado.
No te preocupes, la suma y diferencia de ángulos no es un tema difícil y, principalmente, se basa en la representación de los ángulos.
¿No sabes cómo marcar los ángulos correctamente? ¡Ve a practicar la representación de ángulos y regresa con el 90% de éxito!
Miremos el siguiente ejemplo
Podremos decir que:

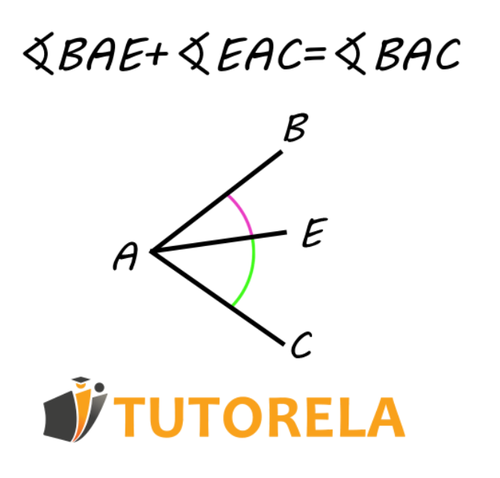
Es sabido que el todo está compuesto por la suma de sus partes, así también ocurre con los ángulos.
El ángulo grande A) está compuesto por los dos ángulos que contiene.
Si sumamos los 2 ángulos que componen el ángulo A) obtendremos este ángulo.
Si conocemos el tamaño de los ángulos podremos, con una operación matemática sencilla, descubrir el valor real del ángulo A).
Por ejemplo, teniendo lo siguiente:
y nos pidieran calcular:
que en realidad es el ángulo grande A) que contiene a los dos ángulos dados en su interior,
todo lo que tenemos que hacer es sumar los valores de los ángulos dados y encontrar el que nos pidieron descubrir.
Podremos decir que:
Diferencia entre ángulos
Del mismo modo que hemos sumado los ángulos también podremos restar uno de otro.
Observemos el siguiente ejemplo:
Si sabemos que:
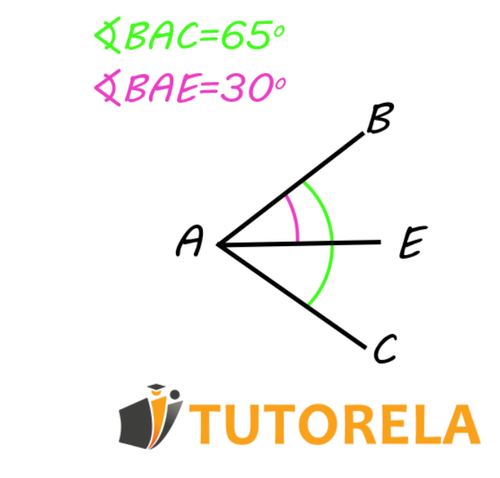
¿Cuál será el valor de ?
Ya que el ángulo contiene a los ángulos y y está compuesto sólo por estos dos,
podremos restar del ángulo mayor a dado y descubrir el ángulo .
Es decir:
Recuerda: ¡El todo está compuesto por la suma de sus partes!
Podemos sumar y restar ángulos que se encuentran sobre el mismo vértice sin ningún problema.
Sólo hay que prestar atención para hacerlo de la forma correcta y saber leer los nombres de los ángulos.
Si está interesado en aprender más sobre otros temas de ángulos, puede ingresar a uno de los siguientes artículos:
- Notación de ángulos
- Lados, vértices, y ángulos
- Bisectriz
- Ángulo recto
- Ángulos adyacentes
- Ángulos opuestos por el vértice
- Ángulos alternos
- Ángulos correspondientes
- Suma de los ángulos de un triángulo
- Suma de los ángulos de un polígono
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Indica qué ángulo es mayor
Indica qué ángulo es mayor
Indica qué ángulo es mayor
Ejercicios de suma y diferencia de ángulos
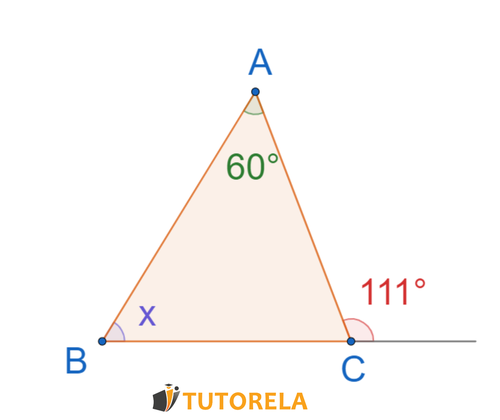
Ejercicio 1
Consigna
Calcula el valor de
Solución
Calculamos a
Ahora calculamos a
Recordemos que la suma de todos los ángulos de un triángulo es igual a
Respuesta
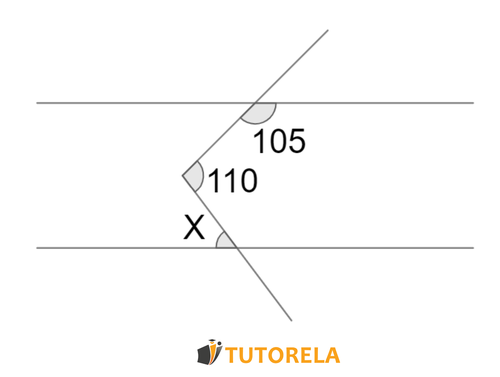
Ejercicio 2
Consigna
Dados los ángulos entre rectas paralelas en la gráfica, ¿cuál es el valor de: ?
Solución
Despejamos y pasamos el
Respuesta
Indica qué ángulo es mayor
Indica qué ángulo es mayor
¿Cuál es la medida del ángulo ABC?
Ejercicio 3
Consigna
Dadas las rectas paralelas
Halla el ángulo
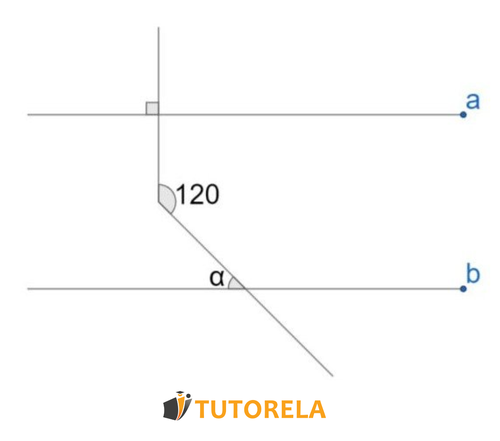
Solución
Continuamos la línea vertical hasta el final y denominamos a los ángulos adyacentes y: cuando de izquierda y: de derecha
Ahora notaremos que el ángulo es un ángulo correspondiente a: y dado que los ángulos adyacentes son iguales a: entonces también el ángulo es igual a:
El ángulo restante en el pequeño triángulo que creamos, que también es el ángulo adyacente a: se llama
Como es un ángulo adyacente a: será igual a: ya que es complementario a:
Ahora calculamos la suma de los ángulos en el triángulo pequeño:
Reemplzamos los datos que sabemos
Movemos las secciones
Respuesta
Ejercicio 4
Consigna
es un triángulo
Según los datos, ¿cuál es el tamaño del ángulo
de valor ?
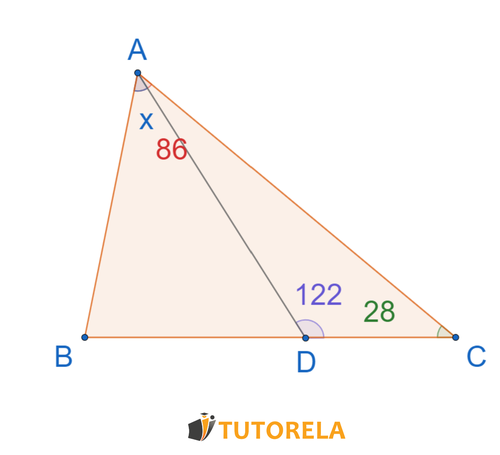
Solución
Primero calculamos el ángulo
Ahora hallemos el ángulo
Ahora nos referimos al triángulo
Respuesta
Halla la medida del ángulo \( \alpha \)
¿Cuál es la medida del ángulo ABC?
Se sabe que el ángulo DBC es igual a 100 grados
¿Cuál es el valor del ángulo vacío?
Ejercicio 5
Consigna
Calcula los valores de y
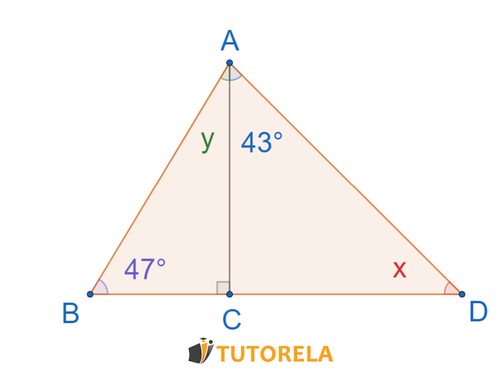
Solución
Nos referimos al triángulo
Hallemos el ángulo
Ahora nos referimos al triángulo
Hallemos el ángulo
Respuesta
Halla la medida del ángulo \( \alpha \)
Halla la medida del ángulo \( \alpha \)
Halla la medida del ángulo \( \alpha \)
ejemplos con soluciones para Suma y diferencia de angulos
Ejercicio #1
Halla la medida del ángulo
Solución en video
Solución Paso a Paso
Recuerda que la suma de los ángulos en un triángulo es igual a 180 grados.
Por lo tanto, usaremos la siguiente fórmula:
Ahora insertemos los datos conocidos:
Simplificamos la expresión y mantenemos el signo apropiado:
Respuesta
80
Ejercicio #2
Dada las medidas de los ángulos: 60,50,70
¿Es posible que estas sean las medidas de los ángulos en cualquier triángulo?
Solución en video
Solución Paso a Paso
Recuerda que la suma de los ángulos en un triángulo es igual a 180 grados.
Sumemos los tres ángulos para ver si su suma es igual a 180:
Por lo tanto, es posible que estos sean los valores de los ángulos en algún triángulo.
Respuesta
Posible
Ejercicio #3
¿Puede un triángulo tener más de un ángulo obtuso?
Solución en video
Solución Paso a Paso
Si tratamos de trazar dos ángulos obtusos y conectarlos para formar un triángulo (es decir, solo 3 lados) parece que esto no es posible.
La respuesta es no.
Respuesta
No
Ejercicio #4
En un triángulo rectángulo, ¿la suma de los dos ángulos no rectos es ?
Solución en video
Solución Paso a Paso
En un triángulo rectángulo hay un ángulo igual a 90 grados, los otros dos ángulos suman 90 grados (180° es la suma de los ángulos en un triángulo)
Por lo tanto, la suma de los dos ángulos no rectos es 90 grados.
Respuesta
90 grados
Ejercicio #5
Dado el triángulo equilátero, halla X
Solución en video
Solución Paso a Paso
Dado que es un triángulo equilátero, todos los ángulos también son iguales.
Como la suma de los ángulos en un triángulo es 180 grados, cada ángulo es igual a 60 grados. (180:3=60)
De ello se deduce que:
Dividimos ambos lados por 8:
Respuesta
7.5
Más preguntas
- Líneas paralelas (Rectas paralelas)
- Ángulos en rectas paralelas
- Ángulos alternos
- Ángulos correspondientes
- Ángulos colaterales
- Ángulos opuestos por el vértice
- Ángulos adyacentes
- Altura del triángulo
- Rectas perpendiculares
- Deltoide
- Área del deltoide:
- Lados, vértices, y ángulos
- Notación de ángulos
- Bisectriz
- Ángulo recto
- Ángulo agudo
- Ángulo obtuso
- Ángulo plano
- Suma de los ángulos internos de un triángulo
- Los lados o aristas de un triángulo
- Paralelogramo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Perímetro de un paralelogramo
- Trapecios
- Área de un trapecio
- Perímetro de un trapecio
- Rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Ángulo exterior de un triángulo
- Área
- Perímetro
- Triángulo
- Tipos de triángulos
- Triángulo obtuso
- Triángulo equilátero
- Identificación de un triángulo isósceles
- Triángulo escaleno
- Triángulo agudo
- Triángulo isósceles
- Área de un triángulo
- Área de un triángulo rectángulo
- Área del triángulo isósceles
- Área del triángulo escaleno
- Área del triángulo equilátero
- Perímetro de un triángulo
- Áreas de Polígonos para 7º Grado
- Triángulo Rectángulo
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- Ángulos exteriores correspondientes
- Ángulos alternos internos
- Mediana en un triángulo
- Centro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Todos los términos en el cálculo de triángulos
- ¿Cómo calcular el área de un triángulo usando trigonometría?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones









