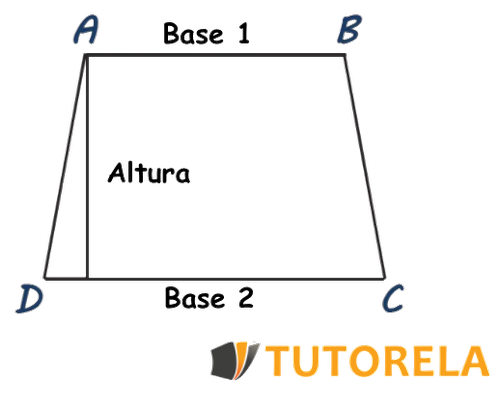
Para calcular el área de un trapecio, necesitas los siguientes tres datos.
- La longitud de la base menor
- La longitud de la base mayor
- La altura entre las bases
La fórmula que debes utilizar para calcular el área de un trapecio es la siguiente:
La suma de las bases multiplicada por la altura y el resultado dividido entre dos.
Fórmula del trapecio: