Ejercicios de Perímetro de Trapecio - Práctica y Problemas

Domina el cálculo del perímetro de trapecios con ejercicios paso a paso, problemas resueltos y fórmulas. Ideal para estudiantes de secundaria.

📚¡Practica el Cálculo del Perímetro de Trapecios!
  • Aplicar la fórmula de perímetro sumando todos los lados del trapecio
  • Resolver problemas con lados desconocidos usando ecuaciones algebraicas
  • Calcular perímetros en trapecios isósceles y rectángulos complejos
  • Usar el teorema de Pitágoras para encontrar lados faltantes
  • Identificar propiedades de trapecios para completar datos ausentes
  • Resolver ejercicios de nivel secundario con confianza y precisión

Entendiendo la Perímetro del trapecio

Explicación completa con ejemplos

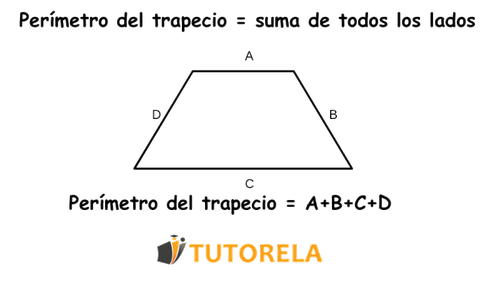
El trapecio es un cuadrilátero definido por la cualidad de tener 2 lados opuestos paralelos. El cálculo del perímetro del trapecio se resuelve utilizando una fórmula muy sencilla que veremos a continuación: se suman todos los lados. Este tipo de preguntas pueden aparecer en pruebas del primer y segundo nivel en los primeros años de la secundaria y también en exámenes finales de nivel 3, 4 y 5 para el egreso del ciclo secundario.

 Perıˊmetro del  trapecio=suma de todos los lados \text{ Perímetro~del~ trapecio=suma~de~todos~los~lados}

Imagen El_calculo_del_perimetro_del_trapecio_se_res.

Explicación completa

Practicar Perímetro del trapecio

Pon a prueba tus conocimientos con más de 12 cuestionarios

Dado el trapecio de la figura, ¿cuál es su perímetro?

7.57.57.54441.51.51.5333

ejemplos con soluciones para Perímetro del trapecio

Soluciones paso a paso incluidas
Ejercicio #1

Dado el trapecio de la figura, ¿cuál es su perímetro?

444555999666

Solución Paso a Paso

Para hallar el perímetro sumaremos todos los lados:

4+5+9+6=9+9+6=18+6=24 4+5+9+6=9+9+6=18+6=24

Respuesta:

24

Solución en video
Ejercicio #2

Dado un trapecio isósceles, calcula su perímetro

666101010121212AAABBBCCCDDD

Solución Paso a Paso

Dado que se trata de un trapecio isósceles y los dos lados son iguales, se puede afirmar que:

AB=CD=6 AB=CD=6

Ahora sumamos todos los lados para hallar el perímetro.

6+6+10+12= 6+6+10+12=

12+22=34 12+22=34

Respuesta:

34

Solución en video
Ejercicio #3

Dado el trapecio de la figura

Dado que la base larga es mayor por 1.5 que la corta

Halla el perímetro del trapecio

222333555

Solución Paso a Paso

Primero calculamos la base larga a partir de los datos existentes:

Multiplique la base corta por 1.5:

5×1.5=7.5 5\times1.5=7.5

Ahora sumaremos todos los lados para hallar el perímetro:

2+5+3+7.5=7+3+7.5=10+7.5=17.5 2+5+3+7.5=7+3+7.5=10+7.5=17.5

Respuesta:

17.5

Solución en video
Ejercicio #4

Dado que el perímetro del trapezoide en el dibujo es 25 cm, halla el lado que falta

777444111111

Solución Paso a Paso

Reemplazamos los datos en la fórmula para hallar el perímetro:

25=4+7+11+x 25=4+7+11+x

25=22+x 25=22+x

25−22=x 25-22=x

3=x 3=x

Respuesta:

3 3 cm

Solución en video
Ejercicio #5

Dado que X=3

Calcula el perímetro del trapecio

XXX101010X+1X+1X+16+X6+X6+XAAABBBCCCDDD

Solución Paso a Paso

Para calcular el perímetro sumamos todos los lados:

10+x+(6+x)+(x+1) 10+x+(6+x)+(x+1)

Ahora dado que x es igual a 3 reemplazamos en los lugares correspondientes:

10+3+(6+3)+(3+1)= 10+3+(6+3)+(3+1)=

10+3+9+4= 10+3+9+4=

13+13=26 13+13=26

Respuesta:

26

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Perímetro del trapecio

¿Cuál es la fórmula para calcular el perímetro de un trapecio?

+
La fórmula del perímetro de un trapecio es: P = a + b + c + d, donde a, b, c y d son las medidas de los cuatro lados. Simplemente suma todas las longitudes de los lados del trapecio para obtener su perímetro.

¿Cómo encontrar un lado faltante del trapecio si conozco el perímetro?

+
Para encontrar un lado faltante: 1) Suma los lados conocidos, 2) Resta esta suma del perímetro total, 3) El resultado es la medida del lado faltante. Por ejemplo: si P=30 y los lados conocidos suman 22, entonces el lado faltante mide 8.

¿Qué diferencia hay entre calcular el perímetro y el área de un trapecio?

+
El perímetro es la suma de todos los lados (P = a + b + c + d), mientras que el área calcula la superficie interior usando la fórmula A = (base mayor + base menor) × altura ÷ 2. Son conceptos completamente diferentes.

¿Puedo usar el teorema de Pitágoras para calcular lados de un trapecio?

+
Sí, cuando el trapecio está inscrito en un rectángulo o triángulo, puedes usar el teorema de Pitágoras (a² + b² = c²) para calcular los lados oblicuos si conoces la altura y las diferencias entre las bases.

¿Qué propiedades del trapecio debo recordar para resolver ejercicios?

+
Propiedades clave: • Un trapecio tiene exactamente dos lados paralelos (bases) • En trapecios isósceles, los lados no paralelos son iguales • La altura es perpendicular a las bases • Estas propiedades te ayudan a completar datos faltantes en los problemas.

¿En qué exámenes aparecen problemas de perímetro de trapecio?

+
Los problemas de perímetro de trapecio aparecen en: exámenes de 1° y 2° de secundaria, pruebas finales de 3°, 4° y 5° año, y evaluaciones de geometría básica. Son fundamentales para comprender cuadriláteros.

¿Cómo resolver ejercicios complejos con trapecios dentro de triángulos?

+
Pasos para ejercicios complejos: 1) Identifica las figuras geométricas involucradas, 2) Usa propiedades de triángulos isósceles si aplica, 3) Aplica teorema de Pitágoras para encontrar lados, 4) Suma todos los lados del trapecio para obtener el perímetro.

¿Qué errores comunes debo evitar al calcular perímetros de trapecios?

+
Errores frecuentes: • Confundir perímetro con área • Olvidar sumar todos los cuatro lados • No usar las propiedades del trapecio para completar datos • Errores aritméticos en la suma final. Siempre verifica que hayas sumado los cuatro lados correctamente.

Continúa tu viaje matemático

Domina primero la Perímetro del trapecio, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas sugeridos para practicar con anticipación

Área de un trapecioÁreaÁreas de Polígonos para 7º GradoÁrea de un trapecio rectánguloÁrea de un trapecio isósceles¿Cómo calculamos el área de figuras complejas?

Temas que se aprenden en secciones posteriores

TrapeciosPerímetro¿Cómo calculamos el perímetro de los polígonos?

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones
Aplicación de la fórmula Calcular el lado faltante basado en la fórmula Comparación entre 2 de la misma forma con un perímetro idéntico Encontrar el área de la base en el perímetro y viceversa Uso de variables