Números enteros

En este artículo aprenderás todo lo necesario sobre los números enteros y lo pondrás en la práctica en varios ejercicios.
¿Comenzamos?

Un número entero es un número positivo o negativo que no es fracción, es decir, está entero.
Nota: Para que un número sea un número entero la única condición es que no sea fracción ni decimal. Solamente un número entero, no importa si es positivo o negativo.
En ejercicios matemáticos utilizamos números enteros casi todo el tiempo, podemos usarlos en operaciones de suma, resta, multiplicación o división.
¿Y qué hay con respecto al $0$?
$0$ también es un número entero.
Hay infinidad de números enteros: todos los números enteros positivos y negativos, desde el infinito de los negativos hasta el infinito de los positivos, son números enteros.

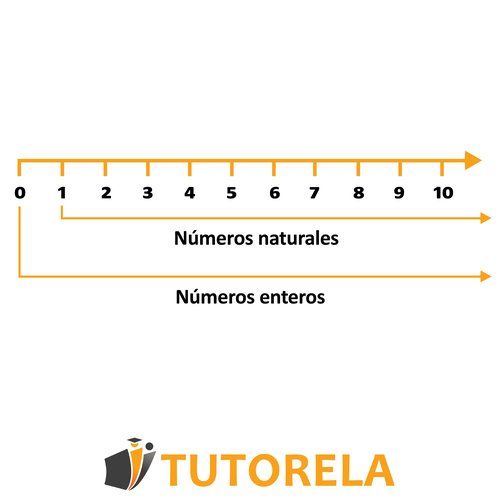
Y ahora ¿qué hacemos? ¡Practiquemos!
Encuentra los números enteros dentro del siguiente conjunto:

$21, 0, -4, \frac{1}{2}$

Solución:
Acorde a su definición, un número entero es cualquier número positivo o negativo que no es fracción. Entonces:
$21$ : Número entero – entero y positivo.
$0$ : Número entero - está incluido dentro del conjunto de los números enteros.
$-4$ :Número entero – entero y negativo.
$\frac{1}{2}$ : Número que no es entero - fracción. 
No tiene importancia que sea positivo o negativo, si es una fracción ya no puede ser un número entero.

Encuentra los números enteros dentro del siguiente conjunto:

$1, -15, -1, \frac{9}{6}$

Solución:
Acorde a su definición, un número entero es cualquier número positivo o negativo que no es fracción. Entonces:
$1$ : Número entero – entero y positivo
$-15$ : Número entero – entero y negativo
$-1$ : Número entero – entero y negativo  
$\frac{9}{6}$ Número que no es entero - fracción. 
No influye para nada que se puedan sacar enteros de esta fracción, un número entero es uno totalmente entero.

Encuentra los números naturales dentro del siguiente conjunto:

$4.5, 1.00000001, 13, \frac{24}{5}$

Solución:
$4.5$: Número que no es entero - decimal.
$1.00000001$: Número que no es entero - decimal
$13$: Número entero – positivo y además entero
$\frac{24}{5}$ : Número que no es entero - aunque aquí hay $2$ enteros, también hay una fracción, por lo tanto, no se lo puede considerar un número entero.

Ahora que ya sabemos identificar números enteros pasaremos a los ejercicios pertinentes:

Encuentra qué hay en el cuadrado:
$(18+2) *⬜ +5=45$

Solución:
En este ejercicio sólo hay números enteros, tenemos que descubrir cuál debería aparecer en lugar del cuadrado.
Primeramente, descubramos cuál es el resultado de los paréntesis y volvamos a escribir el ejercicio. Obtendremos::
$20*⬜ +5=45$
Ahora podemos decir que:$20$ multiplicado por algo $+5$ equivale a $45$.
Si restamos $5$ de ambos miembros nos dará que:
$20*⬜=40$
Ahora pensemos, qué número multiplicado por $20$ nos dará $40$.
También podríamos simplemente dividir ambos miembros por $20$ y obtener:
$⬜=2$

Otro ejercicio con números naturales:
El precio total de una jarra y $4$ vasos es $252 ₪$.
El precio de una jarra equivale al precio de $2$ vasos.

1. ¿Cuál es el precio de la jarra sola?
2. ¿Cuál es el precio de un vaso solo?

Solución:
Sabemos que el precio de la jarra equivale al de $2$ vasos.
Si denominamos el precio de un vaso $X$ podremos decir que el precio de la jarra es $2X$.
También sabemos que una jarra más $4$ vasos cuestan $252 ₪$ .
Lo escribiremos en forma de ejercicio y obtendremos:
$2X+4x=252$
Al resolver la ecuación nos dará que:
$6X=252$
$X=42$

Presta atención: $X$ representa el precio de un vaso.
$2X$  es el precio de una jarra.
Si $X=42$
entonces la respuesta será:
El precio de una sola jarra es $84 ₪$.
$42*2=84$
El precio de un solo vaso es $42 ₪$.