El paralelogramo es un polígono de cuatro lados (cuadrilátero) en el que los lados opuestos son paralelos e iguales en longitud. Una característica clave de los paralelogramos es que tienen dos conjuntos de líneas paralelas, lo que les da su nombre. Ejemplos de paralelogramos incluyen los cuadrados, rectángulos y rombos, que son tipos específicos de paralelogramos con propiedades adicionales únicas.
Conceptos básicos sobre el tema del paralelogramo
- Lados opuestos en un cuadrilátero : son lados que no tienen un punto de encuentro común.
- Lados adyacentes en un cuadrílatero : son lados que tienen un punto de encuentro común.
- Ángulos adyacentes : son 2 ángulos que tienen un vértice y un lado en común.
- Ángulos opuestos en el cuadrilátero son ángulos que no tienen lados comunes.
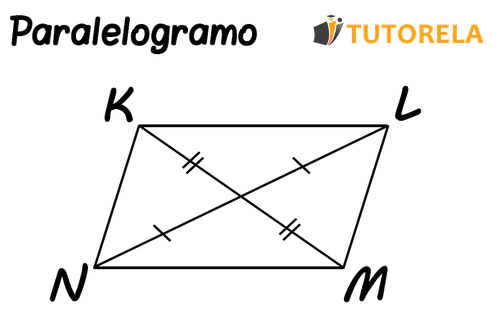
- Diagonal : es una sección que conecta 2 vértices no adyacentes (y no es un lado )
Si el dato es:
Entonces: es un paralelogramo