Números naturales

En este artículo aprenderás todo lo necesario sobre números naturales y lo pondrás en la práctica en varios ejercicios.
¿Comenzamos?

Un número natural debe ser entero y positivo.
Observa: Para que se considere natural a algún número, éste debe cumplir ambas condiciones, ser positivo y entero.
En la vida diaria utilizamos números naturales todo el tiempo, casi cada vez que tenemos que contar o calcular algo.
¿Y qué pasa con el $0$?
$0$ también es un número natural.
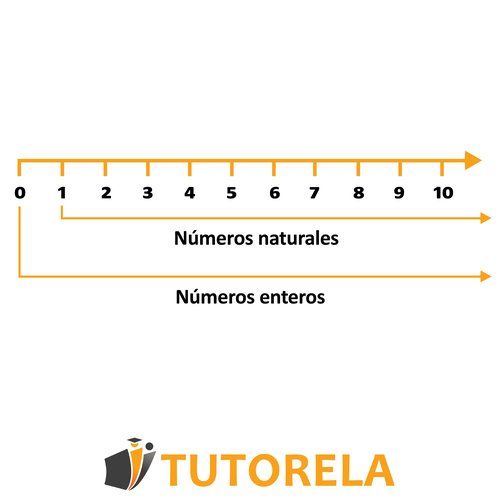
Los números naturales son infinitos: Todos los números positivos enteros desde el $0$ hasta el infinito se denominan números naturales.
Con ellos podemos contar todo lo que queramos y también sumar, restar, multiplicar y dividir.

$21, 0, -4, 7$

Solución:
Acorde a su definición, un número natural es un número entero y positivo. Por consiguiente:
$21$ : Número natural –> entero y positivo.
$0$ : Número natural –> está incluido dentro del conjunto de números naturales.
$-4$ : Número que no es natural –> es negativo (no cumple con la condición de ser positivo)
$7$ : Número natural–> entero y positivo.

$1, -15, -\frac{2}{3}, \frac{7}{6}$

Solución:
Acorde a su definición, un número natural es un número entero y positivo.

Por consiguiente:
$1$  Número natural – entero y positivo.
$-15$  Número que no es natural - es negativo (no cumple con la condición de ser positivo)
$-\frac{2}{3}$  Número que no es natural - negativo y además no es entero
$\frac{7}{6}$  Número que no es natural - No es entero

$2\frac{4}{5} , 13 , -100 , 4.5$

Solución:
$4.5$  Número que no es natural - Si bien es positivo, no es entero.
$-100$ Número que no es natural - Es negativo (no cumple con la condición de ser positivo)
$13$  Número natural – Positivo y además entero
$2\frac{4}{5}$   Número que no es natural - Si bien es positivo, no es entero.

$(2+3) \times ⬜ +15=40$

Solución:
En este ejercicio sólo hay números naturales, tenemos que descubrir cuál correspondería en el sitio del cuadrado.
Primeramente, descubramos cuál es el resultado de los paréntesis y volvamos a escribir el ejercicio.

Obtendremos:
$5 \times ⬜ +15=40$
Ahora podemos decir que $5$  por algo $15 +$ equivale a $40$.
Si restamos $15$ de ambos miembros nos dará que:
$5 \times ⬜ =25$
Ahora pensemos, qué número multiplicado por cinco nos dará $25$.
También podríamos simplemente dividir ambos miembros por $5$ y obtener: 
$5 = ⬜$

El precio general de un par de pantalones y cuatro camisas es $600$$.
El precio de un par de pantalones equivale al precio de $2$ camisas.

1. ¿Cuál es el precio de un par de pantalones?
2. ¿Cuál es el precio de una camisa?

Solución:
Primero acomodemos los datos.
Sabemos que el precio de un par de pantalones equivale al precio de 2 camisas.
Si denominamos el precio de una camisa $X$ podremos decir que el precio de un par de pantalones es $​​2X$.
También sabemos que un par de pantalones y $4$ camisas cuestan $600$$ .
Lo escribiremos en forma de ejercicio y obtendremos:
$2X+4x=600$
Resolvamos la ecuación y nos dará:
$6X=600$
$X=100$

Observa –> $X$ representa el precio de $1$ camisa.
$​​2X$ es el precio de un par de pantalones $1$.
Si $X=100$ entonces la respuesta será:
El precio de un par de pantalones es $200$$.
$100 \times 2=200$
El precio de una camisa es $100$$.