El radio es uno de los tantos elementos que existen en las circunferencias. El radio es un segmento que conecta el centro de la circunferencia con cualquier punto ubicado sobre la circunferencia misma. Cada circunferencia cuenta con un número infinito de radios y su longitud es exactamente la misma, es decir, son idénticos.
El radio nos sirve para calcular el diámetro y el perímetro de la circunferencia, también se utiliza para obtener el área del círculo.
A continuación, hay varios ejemplos de diferentes circunferencias.
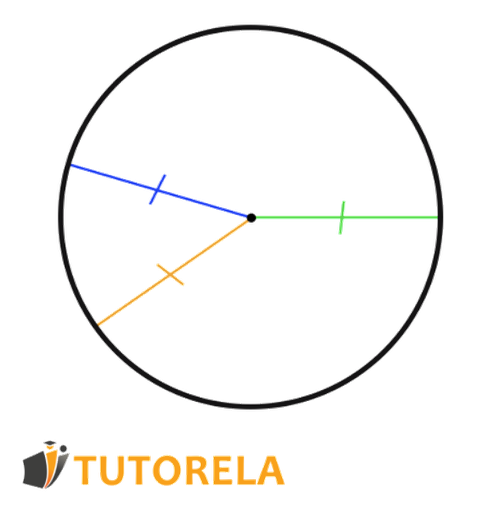
Las partes coloreadas son, de hecho, algunos radios pintados en cada circunferencia:
Las partes coloreadas son, de hecho, algunos radios pintados en la circunferencia: