Propiedades de raíces

1. ¡El resultado de la raíz siempre será positivo! Nunca se obtendrá un resultado negativo. Podemos obtener un resultado de $0$.
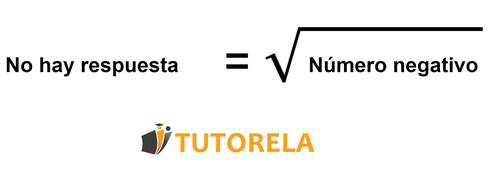
2. Para $\sqrt{}$ de número-negativo ¡No hay respuesta!
3. La raíz es básicamente una potencia media. Podemos decir que: $\sqrt{a}=a^{\frac{1}{2}}$
4. Una raíz que precede a las cuatro operaciones aritméticas. Primero, realice la raíz y solo luego ordene las operaciones de la cuenta.

Las leyes de los radicales son muy relevantes para resolver ejercicios, y combinarlas con reglas de potencias puede ayudarte mucho a resolver ejercicios fácilmente.

Cuando la raíz aparece en todo el producto, podemos desarmar cada factor y aplicarle la raíz dejando el signo de multiplicación entre los factores.
Formulamos:
$\sqrt{(a\cdot b)}=\sqrt{a}\cdot\sqrt{b}$

Cuando aparece la raíz sobre el cociente entero (sobre la fracción entera), podemos desarmar cada factor y activar la raíz sobre él dejando el signo de la división (línea de fracción) entre los factores.
Formulamos:
$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$

La raíz sobre otra raíz, multiplicaremos el orden de la primera raíz por el orden de la segunda raíz y el orden que obtenemos la ejecutaremos como raíz en nuestro número. (Como la norma de potencia sobre otra potencia)
Pongámoslo de esta manera:
$\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\cdot m]{a}$

Una raíz está simbolizada con el signo $√$
De hecho, cuando vemos un número con una raíz, nos preguntamos qué número positivo elevado a $2$, nos dará lo que está escrito dentro de la raíz.
Una raíz es lo contrario de una operación de potencias. Cuando no hay un número pequeño en la parte superior izquierda de la raíz, se denota que es raíz de $2$, raíz cuadrada.
Si aparece un número pequeño a la izquierda, este será el orden de la raíz.

Conozcamos algunas de las leyes fundamentales:

1. ¡¡El resultado de raíz siempre será positivo!! Nunca se obtendrá un resultado negativo. Podemos obtener un resultado de $0$.
2. Para $√$ (número negativo) no hay respuesta!
3. La raíz es básicamente una potencia media. Podemos decir que: $\sqrt a=a^{ 1 \over 2}$
4. Una raíz precede a las cuatro operaciones aritméticas. Primero, realice la raíz y solo luego ordene las operaciones aritméticas.

Veamos el ejemplo:
$\sqrt {64} =8$

Preguntemos, ¿qué número de potencia? $2$ nos dará $64$ y la respuesta es $8$.
Cierto, también $-8$ en potencia $2$ nos dará $64$ ¡pero el resultado de la raíz debe ser positivo!

Cuando encontramos una raíz que está en la totalidad del producto, podemos descomponer los factores del producto y dejar una raíz separada para cada uno de ellos.
Formularemos esto como regla:
$\sqrt{(a\cdot b)}=\sqrt{a}\cdot\sqrt{b}$

Veamos esto en el ejemplo:
$\sqrt{(64\cdot100)}$
Según la regla de la raíz de un producto, podemos descomponer los factores y dejar la raíz de cada factor por separado manteniendo la operación de multiplicación entre ellos:
Lo descompondremos y obtendremos:
$\sqrt{64}\cdot\sqrt{100}=$
$8\cdot10=80$

Cuando nos encontramos con una raíz que está en todo el cociente (fracción) podemos descomponer los factores del cociente y dejar para cada uno de ellos una raíz separada. Dejaremos entre los dos factores la operación de división: la línea de fracción.

Formulemos de esta manera:$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$

Veamos esto en el ejemplo:

$\sqrt{\frac{36}{9}}$

Según la regla de la raíz de un cociente, podemos descomponer los factores y dejar la raíz de cada factor por separado manteniendo la operación de multiplicación entre ellos:
Descompondremos y obtendremos:

$\frac{\sqrt{36}}{\sqrt{9}}$

$\frac{6}{3}=2$

Cuando nos encontramos con un ejercicio donde hay una raíz sobre una raíz, multiplicaremos el orden de la primera raíz por el orden de la segunda raíz y el orden que obtendremos lo multiplicaremos como raíz sobre nuestro número. (Como en la regla de potencia sobre potencia)
Formulemos de esta manera:
$\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\cdot m]{a}$

Veamos esto en el ejemplo: 
$\sqrt[2]{\sqrt[4]{100}}=\sqrt[2\cdot4]{100}=\sqrt[8]{100}$

Si te interesa este artículo también te pueden interesar los siguientes artículos:

La raíz de un producto

Raíz del cociente

Raíz de una raíz

Combinando potencias y raíces

En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.