En este artículo aprenderemos cómo solucionar ecuaciones fraccionarias. Cuando nos encontremos con una ecuación que tiene un número en el denominador, querremos deshacernos de ese número y conseguir que no haya ningún denominador.
Lo haremos multiplicando ambos miembros de la ecuación por el denominador común más pequeño posible.
En este artículo veremos varios ejemplos de ejercicios con números en el denominador, e iremos ascendiendo gradualmente con los niveles de dificultad.
Los primeros ejercicios serán relativamente simples, tendrán una sola fracción con un número en el denominador. En los siguientes veremos ejercicios con dos o tres fracciones.
Cuando nos encontremos con una ecuación que tiene un número en el denominador, querremos deshacernos de ese número y conseguir que no haya ningún denominador. Lo haremos multiplicando ambos miembros de la ecuación por el denominador común más pequeño posible.
Ejemplos con soluciones de ecuaciones con fracciones
Ejemplo 1
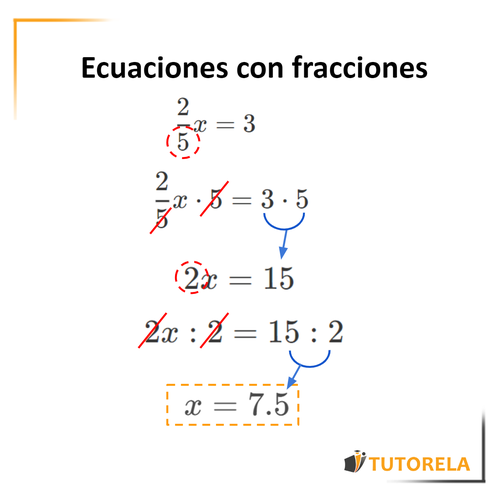
52X=3
En este caso tenemos un 5 en el denominador. Querremos deshacernos de él. Entonces multiplicaremos los dos miembros de la ecuación por el denominador, es decir por cinco.
Se acostumbra a expresarlo de esta manera:
52X=3 /×5
Multiplicaremos por separado cada miembro y obtendremos:
52X×5=3×5
Es decir,
2x=15 /:2
x=7.5
¡Únete a 30,000 estudiantes destacados en matemáticas!
Práctica ilimitada, guía de expertos: mejora tus habilidades matemáticas hoy
Ejemplo 2
31X=2X−4
Multiplicaremos ambos miembros de la ecuación por el denominador, es decir, multiplicaremos por 3 y obtendremos
31X=2X−4 /×3
31X×3=2X×3−4×3
x=6x−12
12=5x
X=512
Ejemplo 3: Ecuación con dos denominadores
32X+1=23X−2+4
En este ejercicio tenemos dos fracciones, o sea, dos denominadores distintos. También aquí nuestro objetivo es deshacernos de los denominadores. Para conseguirlo multipliquemos ambos miembros de la ecuación por el denominador común más pequeño posible. En este caso, el denominador común es 6.
Obtendremos:
32X+1=23X−2+4 /×6
32X+1×6=23X−2×6+4×6
2(2x+1)=3(3x−2)+4×6
4x+2=9x−6+24
−16=5x
X=−516
Ejemplo 4
35X−4X+1=2X+1
Nos gustaría deshacernos del denominador de las dos fracciones, por lo tanto, nuevamente multiplicaremos por el común denominador. El común denominador más pequeño es 12 en este caso.
35X−4X+1=2X+1 /×12
35X×12−(4X+1)×12=2X×12+1×12
20x−3×(x+1)=24x+12
20x−3x−3=24x+12
−15=7x
X=−715
Ejemplo 5
2X+3X=41
También en esta situación querremos deshacernos del denominador. Tenemos que multiplicar por el denominador común más pequeño posible. Veremos que la multiplicación de todos los denominadores juntos nos dará 24, éste es un común denominador que nos podría servir, pero no es el más pequeño y, por lo tanto, no es conveniente usarlo para la multiplicación.
Recordemos que para descubrir el común denominador más pequeño debemos multiplicar entre ellos a todos los factores primos de los números que aparecen en el denominador. En nuestro caso: 24 está compuesto por 2 y 2. 3 es número primo. El 2 también es número primo, incluido, igualmente, dentro del 4.
Por lo tanto, tenemos que multiplicar:
2×2×3=12
O sea, 12 es el común denominador más pequeño posible. Entonces multipliquemos los dos miembros por 12 y obtendremos:
2X+3X=41 /×12
2X×12+3X×12=41×12
6x−4x=3
2x=3
X=23