Unidades de volumen

La función de las unidades de volumen es cuantificar o medir el volumen de los objetos. Ya que se trata de una unidad tridimensional, estas unidades siempre se expresan en potencias terceras.

Por ejemplo, centímetro cúbico \( \operatorname{cm}^3 \) y metro cúbico \( \left(m^3\right) \). Al referirse a líquidos el volumen se suele medir por litros o galones.

Analicemos un ejercicio simple:

Tenemos una caja con las siguientes medidas:

Largo 4 cm

Ancho 5 cm

Altura 6 cm

\( 4\operatorname{cm}\times5\operatorname{cm}\times6\operatorname{cm}=120 \)

\( Largo 4 cm\times ancho 5 cm\times altura 6 cm \)

si debemos calcularle su volumen.

En este caso el cálculo es bastante simple. Calcularemos el volumen de la caja multiplicando las tres medidas entre sí. El resultado es \( 120cm^3 \). Es primordial destacar que, debido a que multiplicamos tres veces cm por cm por cm, el resultado se da en \( \operatorname{cm}^3 \), o sea, cm cúbico (cm elevado a la tercera potencia).

Si te interesa este artículo, también te pueden interesar los siguientes artículos:

En el Blog de Matemáticas de Tutorela puedes encontrar una variedad de artículos de matemáticas

Medidas de volumen

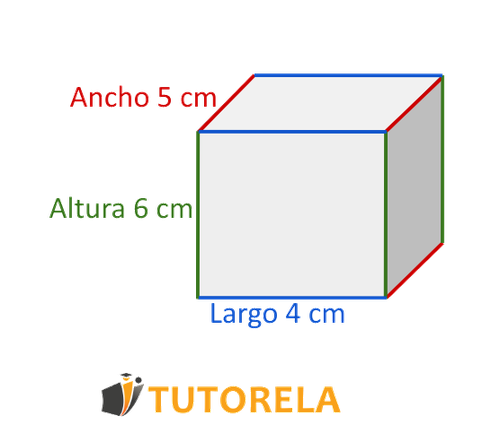
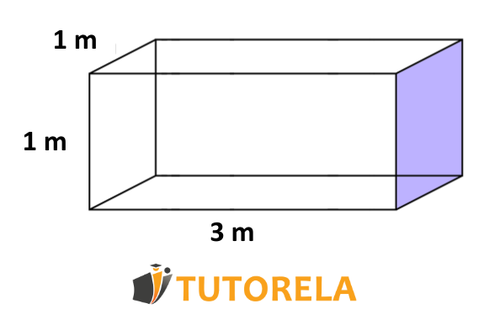
Todo cuerpo tridimensional tiene volumen. Por ejemplo, una pelota o pirámide son cuerpos con volumen. El volumen de un cuerpo es nuestro modo de medir el lugar que dicho cuerpo ocupa en el espacio.

Por ejemplo, observemos un cubo que la longitud de cada uno de sus lados es de \( 1\operatorname{cm} \), como éste:

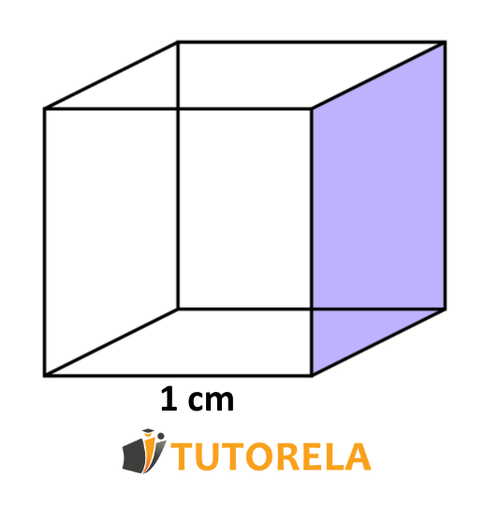
un cubo que la longitud de cada uno de sus lados es de 1 cm

Para calcular el volumen del cubo utilizaremos la fórmula conocida: \( Largo\times ancho\times altura \)

En este caso las tres dimensiones son iguales y, por lo tanto, anotaremos:

\( V=1\operatorname{cm}\times1\operatorname{cm}\times1\operatorname{cm}=1\operatorname{cm}^3 \)

V es la letra que se usa para abreviar la palabra volumen en ejercicios y se utiliza para designar volúmenes.

Es decir, nos dio que el volumen del cubo es \( 1cm³= \) centímetro cúbico (cm elevado a la tercera potencia)

Unidades de medida de volumen que son conocidas:

\( 1m³=1000dm³=1,000,000cm³ \)

\( 1dm³=1000cm³ \)

Además, hay medidas que utilizamos principalmente para medir líquidos:

\( 1 L=1 dm³=1,000 cm³ \)

\( 1 litro=1000 mililitros \)

\( 1 mililitro = 1 cm³ \)

\( 1000 litros=1 m³ \)

Ejemplo 1:

¿Cuántos litros de agua entran en la caja ilustrada?:

Recordemos que la fórmula para calcular el volumen de una caja es:

\( Largo\times ancho\times altura \).

Calculemos el volumen de la caja:

\( V=1m\times1m\times3m=1m^3 \)

\( 1m³=1000dm³=1,000,000cm³ \)

Nos dio que el volumen de la caja es \( 3m³ \) (metros cúbicos).

Ahora debemos convertir el resultado a litros para responder a la pregunta.

Recordemos que \( 1m³=1000 \) litros.

Entonces:

\( 3m³=3000 \) litros.

Es decir, la cantidad de agua que podemos introducir en la caja es 3000 litros.

Ejemplo 2

¿Cuántos litros son \( 10,000cm³ \)?

Recordemos que:

\( 1,000cm³=1litro \)

Entonces:

\( 10,000\operatorname{cm}³=10\times1000\operatorname{cm}³=10\times1Litro=10Litros \)

Es decir, nos dio que \( 10,000cm³ \) equivalen a \( 10 \) litros.