Probabilidad es la posibilidad de llegar a cierto resultado.
Probabilidad para alumnos de 14 años
Probabilidad de sucesos aleatorios independientes
En sucesos aleatorios independientes, cada uno de los sucesos no influye en la probabilidad del otro.
Señalización de sucesos aleatorios independientes
La independencia se señala así
la independencia entre sucesos aleatorios se señala así:
La probabilidad se señala con la letra
Fórmula para calcular la probabilidad de sucesos aleatorios independientes:
El significado de
La probabilidad de que los sucesos aleatorios y ocurran a la vez.
Tabla de doble entrada para encontrar la solución a preguntas de probabilidad
En la tabla habrá dos columnas y dos filas.
Primera columna
indicará la probabilidad de que el primer suceso haya ocurrido
Segunda columna
indicará la probabilidad de que el primer suceso no haya ocurrido
Primera fila
indicará la probabilidad de que el segundo suceso haya ocurrido
Segunda fila
indicará la probabilidad de que el segundo suceso no haya ocurrido
Dentro de la tabla se mostrarán las probabilidades de ambos sucesos respectivamente.
Nota: La probabilidad de que cierto suceso aleatorio ocurra sumado a la probabilidad de que éste no ocurra, siempre dará como resultado.
Cálculo de probabilidad con área en una tabla de doble entrada
Al igual que una tabla de doble entrada, estará compuesta por dos columnas y dos filas.
Anotaremos a lado de cada largo y ancho la probabilidad correspondiente.
El cálculo del área del cuadrado concerniente señalará la probabilidad de que ocurra tanto el suceso indicado en el largo como el indicado en el ancho.
Como dice la fórmula del cálculo, multiplicaremos el largo por el ancho y obtendremos la probabilidad buscada.
Cálculo de probabilidad con dendrograma (diagrama de árbol)
El dendrograma describe el proceso realizado en el experimento.
Saquemos dos ramas que describan la probabilidad de que el primer suceso haya ocurrido y la probabilidad de que el primer suceso no haya ocurrido.
Desde las ramas que trazamos, saquemos de cada una de ellas otro par de ramas que describan la probabilidad de que el segundo suceso haya ocurrido y la probabilidad de que el segundo suceso no haya ocurrido.
Para hallar la probabilidad que describe lo que ha ocurrido en el primer suceso y también lo que ha ocurrido en el segundo, multiplicaremos las probabilidades correspondientes representadas en las ramas.
Sucesos aleatorios dependientes
En sucesos aleatorios dependientes, cada suceso influye en la probabilidad de ocurrencia del otro.
Probabilidad condicional
La probabilidad condicional hace referencia al caso de que tengamos algún dato que pudiera modificar la probabilidad de que cierto suceso haya ocurrido.
Probabilidad
Antes de que comencemos a hablar de la probabilidad de sucesos aleatorios independientes, de la probabilidad de sucesos aleatorios dependientes y de la probabilidad condicional, recordemos qué es la probabilidad misma.
¿Qué es la probabilidad?
Probabilidad es la posibilidad de obtener un resultado específico.
De hecho, puedes cambiar la palabra probabilidad por posibilidad y llegar al mismo significado.
Probabilidad de sucesos aleatorios independientes
¿Qué son los sucesos aleatorios independientes?
Sucesos aleatorios independientes son sucesos que ocurren sin ser afectados por otros sucesos. Ningún suceso influye en la probabilidad de que otro suceso ocurra o no. De hecho, podemos decir en un idioma muy simple, que la ocurrencia de cierto suceso no influye en la posibilidad de que otro suceso ocurra ya que no dependen uno de otro.
Hay muchos ejemplos de la vida diaria en los que podemos observar este tipo de sucesos aleatorios independientes, por ejemplo:
Suceso primero – ha llovido
Suceso segundo – salió en el dado
Podemos decir, con total certeza, que no hay ninguna relación entre que haya llovido y que haya salido un en el dado.
El símbolo de sucesos aleatorios independientes es
Si deseamos indicar que los sucesos y son independientes lo señalaremos del siguiente modo:
Probabilidad escribiremos con la letra
La probabilidad de sucesos aleatorios independientes equivale al producto de las probabilidades de los dos sucesos por separado. Es decir, la probabilidad del suceso por la probabilidad del suceso .
Veámoslo en la fórmula:
El significado de
La probabilidad de que los sucesos aleatorios y ocurran a la vez.
Por ejemplo, si la probabilidad de que ocurra el primer suceso, que llueva, es
y la probabilidad de que ocurra el segundo suceso, que salga en el dado, es
entonces, las probabilidades de ambos sucesos juntos son:
Observa, en las preguntas en que se describe que se saca algo y luego ese algo se devuelve, los sucesos suelen ser independientes.
Si se describe un caso en el que se quita una pelota y se la devuelve, en realidad, estamos volviendo al punto de partida, por lo que el primer suceso no afecta al segundo.
Veamos un ejemplo de preguntas de este tipo:
Hay pelotas en un cajón. de ellas son rojas y azules.
Dora saca una pelota del cajón y luego la devuelve. Más tarde vuelve a sacar una pelota.
¿Cuál es la probabilidad de que Dora haya sacado dos pelotas azules?
Solución:
Dividiremos el experimento en dos sucesos:
El primer suceso - Sacar la pelota azul por primera vez.
El cálculo para que ocurra este suceso será:
Hay pelotas azules entre las que contiene el cajón.
Por lo tanto, la probabilidad de sacar una azul la primera vez es .
El segundo suceso - Sacar la pelota azul por segunda vez.
También ahora hay pelotas azules entre las que contiene el cajón ya que la primera fue devuelta.
Por lo tanto, la probabilidad de sacar una pelota azul la segunda vez también es .
Para descubrir la probabilidad de que ocurran estos dos sucesos independientes ,
multiplicaremos las probabilidades que obtuvimos según la fórmula y obtendremos:
Distintas maneras para calcular la probabilidad de sucesos aleatorios independientes
Tabla de doble entrada
Tabla de doble entrada para solucionar preguntas de probabilidad:
No le temas. Sólo representa los datos de una forma más clara y sencilla.
La tabla estará compuesta por dos columnas en las que se señalará la probabilidad de que el primer suceso haya ocurrido y la probabilidad de que el primer suceso no haya ocurrido y, de dos filas en las que se describirá la probabilidad de que el segundo suceso haya ocurrido y la probabilidad de que el segundo suceso no haya ocurrido.
Dentro de la tabla se verán las probabilidades para ambos sucesos respectivamente (por ejemplo, uno ocurrió y el otro no)
Es menester que sepas que la probabilidad de que cierto suceso ocurra sumado a la probabilidad de que cierto suceso no ocurra, siempre será .
Ahora, describiremos un excelente ejemplo para el uso de la tabla de doble entrada y así la entenderás mejor:
En un jarrón hay pelotas - una rosa y la otra verde.
En una caja, totalmente diferente, que no tiene ninguna relación con el jarrón, hay tres alhajas - un anillo, un brazalete y un collar.
Diana elije aleatoriamente una pelota del jarrón y luego introduce la mano en la caja y extrae de ella una alhaja.
Anotaremos en la tabla de doble entrada todas las posibilidades que hay al sacar la pelota y al sacar la alhaja y las probabilidades.
Además, determinaremos cuántas posibilidades existen.
| Cajón / jarrón | Pelota verde | Pelota rosa | |
| Anillo | anillo y pelota rosa | anillo y pelota verde | |
| Brazalete | brazalete y pelota rosa | brazalete y pelota verde | |
| Collar | collar y pelota rosa | collar y pelota verde | |
En la tabla vemos que son posibles . resultados.
Si nos pidieran la probabilidad de que salga una posibilidad específica podremos responder con facilidad.
Por ejemplo, si nos preguntan por la probabilidad de que salga una pelota rosa y una alhaja que se usa en la mano –>
parece que hay dos opciones: anillo y pelota rosa o brazalete y pelota rosa.
Por lo tanto, la probabilidad será: .
Es decir, 2 opciones dentro de las 6 posibilidades que hay.
Ahora pasaremos a la segunda manera:
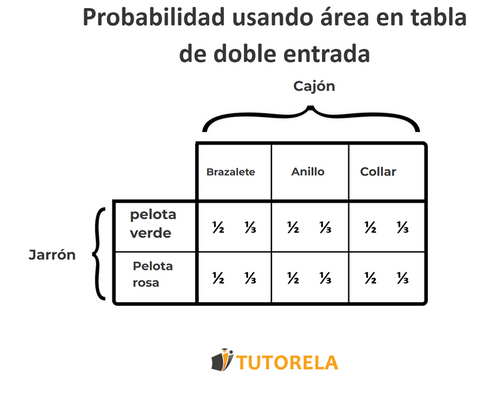
Área en tabla de doble entrada
El cálculo de la probabilidad con área es muy similar al cálculo con tabla de doble entrada, pero nos hace observar más las probabilidades.
Si miramos la tabla de arriba, veremos que los cálculos que anotamos en cada segmento son el cálculo del área.
Veámoslo en un ejemplo más simple y calculemos el área dentro de la tabla:
En realidad, lo que haremos es anotar al lado de cada largo y ancho la probabilidad correspondiente.
El cálculo del área del cuadrado concerniente señalará la probabilidad de que ocurra tanto el suceso indicado en el largo como el indicado en el ancho.
Como en la fórmula de cálculo, multiplicaremos el largo por el ancho y obtendremos la probabilidad buscada.
Si, por ejemplo, queremos calcular la probabilidad de sacar el brazalete y la pelota verde, obtendremos una probabilidad de:
Ahora pasaremos a la tercera manera:
A través de un dendrograma (diagrama de árbol)
El dendrograma es un diagrama muy simpático por el cual describimos las probabilidades de cada suceso.
El árbol describe de un modo estupendo las secuencias del experimento.
Primeramente sacaremos dos ramas que describan la probabilidad de que el primer suceso haya ocurrido y la probabilidad de que el primer suceso no haya ocurrido.
Desde las ramas que trazamos, sacaremos de cada una de ellas otro par de ramas que describan la probabilidad de que el segundo suceso haya ocurrido y la probabilidad de que el segundo suceso no haya ocurrido.
Volvamos al ejemplo de las pelotas de la primera pregunta:
En el cajón hay pelotas de ellas son rojas y azules.
Dora saca una pelota del cajón y luego la devuelve. Más tarde vuelve a sacar una pelota.
¿Cuál es la probabilidad de que Dora haya sacado dos pelotas azules?
Dibujemos la primera salida y las probabilidades de sacar una pelota azul o roja:
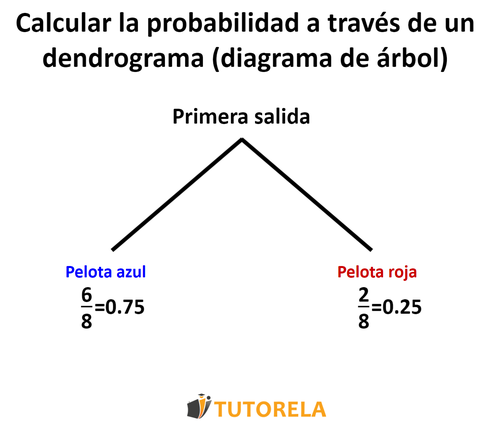
Ahora, seguiremos dibujando la segunda salida de cada rama
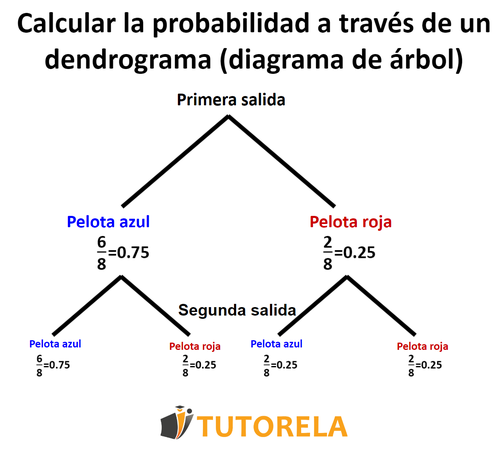
Primera salida
Ahora, cuando nos pregunten sobre la probabilidad de sacar una u otra, sabemos que todo lo que tenemos que hacer es multiplicar las probabilidades correspondientes.
Por ejemplo, si nos preguntan ¿cuál es la probabilidad de sacar una pelota azul la primera vez y una pelota roja la segunda?
Observemos el árbol,
veamos ¿cuál es la probabilidad de sacar una pelota azul en primer lugar? .
Ahora necesitamos la probabilidad de sacar una pelota roja en segundo lugar, luego de que sacamos una azul.
Por lo tanto, iremos a la rama izquierda, la rama de la salida de la pelota azul en el primer intento y veremos que la probabilidad de sacar una pelota roja en el segundo intento es .
Multiplicaremos ambas probabilidades y obtendremos
Sucesos aleatorios dependientes
Sucesos aleatorios dependientes son sucesos en los que existe alguna relación entre la probabilidad de que el primer suceso ocurra y la probabilidad de que ocurra el segundo.
Podremos percibir que se trata de sucesos aleatorios dependientes si se nos presentan problemas que describen que se ha sacado un objeto pero no se ha devuelto, entonces se produce un cambio que altera al segundo suceso.
Asimismo, si se nos presentan problemas de este estilo: si llegara a pasar algo, entonces pasaría otra cosa como resultado del primer suceso, sabremos que se trata de probabilidad condicional.
De hecho, cuando identifiquemos dependencia entre los sucesos entenderemos que son sucesos dependientes.
Un ejemplo de sucesos aleatorios dependientes sacado de la vida diaria es:
Primer suceso - Roni estudió para el examen
Segundo suceso - Roni pasó el examen
Nuestra lógica debe avisarnos de que hay cierta relación entre estos dos sucesos. Si se estudia para el examen o no se estudia para el examen influye en si pasaremos el examen o no.
En los sucesos aleatorios dependientes el dendrograma ayuda a entender la dependencia a través de las raíces y a calcular la probabilidad correcta.
Probabilidad condicional
La probabilidad condicional hace referencia al caso de que tengamos algún dato que pudiera modificar la probabilidad de que cierto suceso haya ocurrido.
Ejemplo de la vida diaria
Si nos preguntasen ¿cuál es la probabilidad de que mañana llueva en la Tierra de Oz?
no sabremos responder.
Pero, si nos brindasen información acerca de que en la Tierra de Oz casi no llueve, la probabilidad que presentaríamos sería diferente.
Veamos un ejemplo un poco más avanzado
En el cuarto grado de una escuela hay niños y niñas.
niñas.
niños.
Parte de los alumnos de la clase participan en un curso de informática y otros no.
estudian informática.
no estudian informática.
Más datos
niños de la clase estudian informática.
y niñas de la clase estudian informática.
Organicemos los datos dentro de la tabla:
| Total | No participan del curso de informática | Participan del curso de informática | |
| 15 | por lo tanto habrá 5 | 10 | niños |
| 25 | por lo tanto habrá 8 | 17 | niñas |
| 40 | 21 | 19 | total |
Ahora, si nos preguntasen sobre la probabilidad de que, al sacar al azar un alumno varón de la clase, sea uno de los que participan en el curso de informática, podremos observar la tabla y ver que ( 10 \)
niños estudian informática dentro de los ( 15 \) niños que hay en la clase y, por consiguiente, la probabilidad será:
La clave para el éxito en ejercicios de probabilidad condicional es identificar los datos que conocemos.
¿seleccionamos un niño?
¿seleccionamos una niña?
o tal vez simplemente ¿seleccionamos participantes del curso de informática?
Lo que sabemos estará en el denominador.
Lo que no sabemos estará en el numerador y significará la parte dentro del dato que conocemos.
Si te interesa este artículo también te pueden interesar los siguientes artículos:
Probabilidad de sucesos aleatorios independientes
Sucesos aleatorios dependientes
En el blog de Tutorela encontrarás una variedad de artículos sobre matemáticas.
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones








