Propiedad asociativa de la suma - Ejemplos, Ejercicios y Soluciones

Entendiendo la Propiedad asociativa de la suma

Explicación completa con ejemplos

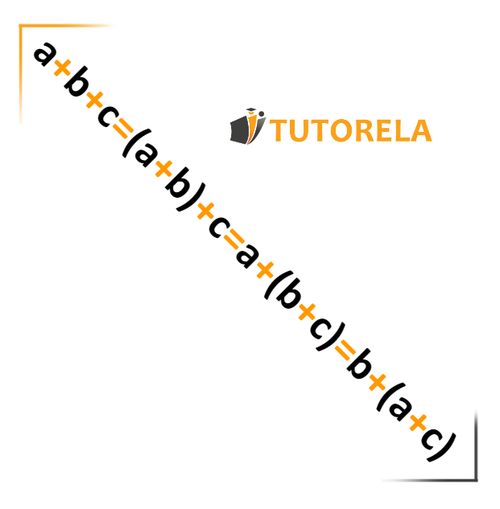
La propiedad asociativa de la suma nos permite agrupar dos sumandos y agregarle al resultado el tercer sumando.
Podemos utilizar esta propiedad de tres maneras:
La primera :
Se unen primero el sumando segundo y el tercero, se resuelve la suma y al resultado se le agrega el primer sumando.
La segunda manera:
Primero sumamos el primer y el segundo sumando, resolvemos la suma y al resultado le agregamos el tercer sumando.

La tercera manera:
primero sumamos el primer y el tercer sumando, resolvemos la suma y al resultado le agregamos el segundo sumando.
Colocaremos entre paréntesis los sumandos que queramos agrupar primero.
La propiedad asociativa de la suma también funciona para expresiones algébricas, pero no para operaciones de restar.
Formulemos la propiedad asociativa de la suma como la siguiente regla:
$a+b+c=(a+b)+c=a+(b+c)=(a+c)+b$

Explicación completa

Practicar Propiedad asociativa de la suma

Pon a prueba tus conocimientos con más de 21 cuestionarios

$$ 6:2+9-4= $$

ejemplos con soluciones para Propiedad asociativa de la suma

Soluciones paso a paso incluidas

Ejercicio #1

$12\times5\times6=$

Solución Paso a Paso

De acuerdo a las reglas del orden de las operaciones aritméticas, resolvemos el ejercicio de izquierda a derecha:

$12\times5=60$

$60\times6=360$

Respuesta:

360

Solución en video

Ejercicio #2

$13+2+8=$

Solución Paso a Paso

Usamos la propiedad conmutativa y primero resolvemos el ejercicio de suma a la derecha:

$2+8=10$

Ahora obtenemos:

$13+10=23$

Respuesta:

23

Solución en video

Ejercicio #3

$2+4-3=$

Solución Paso a Paso

Resolvemos el ejercicio de izquierda a derecha, colocamos el ejercicio de suma entre paréntesis y luego restamos:

$(2+4)-3=$

$6-3=3$

Respuesta:

3

Solución en video

Ejercicio #4

$24:8:3=$

Solución Paso a Paso

Según el orden de las operaciones aritméticas resolvemos el ejercicio de izquierda a derecha ya que la única operación del ejercicio es la división:

$24:8=3$

$3:3=1$

Respuesta:

$1$

Solución en video

Ejercicio #5

$2+6-10+30-2=$

Solución Paso a Paso

Resolvemos el ejercicio de acuerdo al orden de operaciones aritméticas.

Colocamos los ejercicios de suma y resta entre paréntesis de la siguiente manera para facilitar la resolución del ejercicio:

$(2+6)-10+(30-2)=$

Resolvemos los ejercicios entre paréntesis:

$8-10+28=$

Colocamos entre paréntesis el ejercicio de resta:

$(8-10)+28=$

$-2+28=26$

Respuesta:

26

Solución en video

Continúa tu viaje matemático

Domina primero la Propiedad asociativa de la suma, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas sugeridos para practicar con anticipación

La propiedad conmutativa Propiedad conmutativa de la suma Propiedad conmutativa de la multiplicación Propiedad distributiva La propiedad distributiva para alumnos de 1.º de ESO La propiedad distributiva en el caso de las divisiones La propiedad distributiva en el caso de la multiplicación Las propiedades conmutativas, la multiplicación, la propiedad distributiva y ¡otras más!

Temas que se aprenden en secciones posteriores

La propiedad asociativa Propiedad asociativa de la multiplicación Operaciones aritméticas avanzadas: Resta de sumas, resta de diferencias, división por producto y división por cociente Resta de números enteros con paréntesis en los que hay sumas División de números enteros entre paréntesis en los que hay una división Resta de números enteros con paréntesis en los que hay restas División de números enteros entre paréntesis en los que hay una multiplicación

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Más de dos fracciones Solo por multiplicación Solo suma Solo suma y resta Solo suma y resta Suma, resta, multiplicación y división Uso de fracciones Uso de variables