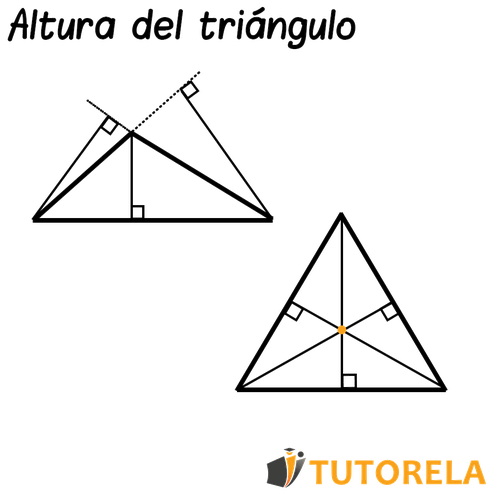
Ejercicios de Altura del Triángulo - Práctica y Problemas

Practica calcular la altura de triángulos con ejercicios paso a paso. Aprende a usar el teorema de Pitágoras y fórmulas de área con problemas resueltos.

📚¿Qué aprenderás practicando altura de triángulos?
  • Calcular la altura de triángulos usando el teorema de Pitágoras
  • Determinar el área de paralelogramos aplicando la altura perpendicular
  • Resolver problemas de triángulos rectángulos con medidas conocidas
  • Encontrar la altura de trapecios usando fórmulas de área
  • Aplicar propiedades de triángulos isósceles en cálculos de altura
  • Identificar alturas interiores y exteriores en diferentes tipos de triángulos

Entendiendo la Partes de un triángulo

Explicación completa con ejemplos

Establecer la altura de un triángulo

La altura de un triángulo es la línea perpendicular que une el vértice con el lado opuesto a él de tal manera que se crea un ángulo de 90 grados. 

En todo triángulo hay tres alturas, ya que hay tres vértices de los cuales se puede calcular la altura con respecto al lado que se encuentra opuesto a cada uno de ellos.

La altura puede encontrarse tanto dentro como fuera del triángulo. Si no pasa por dentro del triángulo, se denomina altura exterior. 

A continuación, te dejamos algunos ejemplos de alturas de triángulos:

altura del triangulo

Explicación completa

Practicar Partes de un triángulo

Pon a prueba tus conocimientos con más de 36 cuestionarios

¿Puede un triángulo tener un ángulo recto?

ejemplos con soluciones para Partes de un triángulo

Soluciones paso a paso incluidas
Ejercicio #1

Dados los dos triángulos, ¿ EC es un lado en uno de los triángulos?

AAABBBCCCDDDEEEFFF

Solución Paso a Paso

Cada triángulo tiene 3 lados, repasaremos el triángulo del lado izquierdo:

Sus lados son: AB,BC,CA

Es decir, en este triángulo el lado EC no existe.

Repasemos el triángulo de la derecha:

Sus lados son: ED,EF,FD

Es decir, en este triángulo el lado EC no existe.

Por lo tanto, EC no es un lado en ninguno de los triángulos.

Respuesta:

No

Solución en video
Ejercicio #2

El triángulo ABC isósceles.

Dada: AD mediana.

¿Cuál es el tamaño del ángulo? ∢ADC ∢\text{ADC} ?

AAABBBCCCDDD

Solución Paso a Paso

En un triángulo isósceles, la mediana a la base es también la altura a la base.

Es decir, el lado AD forma un ángulo de 90° con el lado BC.

Es decir, se nos crean dos triángulos rectángulos.

Por lo tanto, el ángulo ADC es igual a 90 grados.

Respuesta:

90

Solución en video
Ejercicio #3

¿Cuál de las siguientes es la altura en el triángulo ABC?

AAABBBCCCDDD

Solución Paso a Paso

Recordemos la definición de altura:

Una altura es una línea recta que desciende del vértice de un triángulo y forma un ángulo de 90 grados con el lado opuesto.

Por lo tanto, el que forma un ángulo de 90 grados es el lado AB con el lado BC

Respuesta:

AB

Solución en video
Ejercicio #4

Dado el triángulo siguiente:

Anote cuál es la altura del triángulo ABC.

AAABBBCCCEEEDDD

Solución Paso a Paso

Una altura en un triángulo es el segmento que une el vértice y el lado opuesto, de tal manera que el segmento forma un ángulo de 90 grados con el lado.

Si observamos el dibujo, podemos notar que el teorema anterior es cierto para la recta AE que cruza BC y forma un ángulo de 90 grados, sale del vértice A y por lo tanto es la altura del triángulo.

Respuesta:

AE

Solución en video
Ejercicio #5

Determinar si la afirmación es verdadera o falsa.

α+β=180 \alpha+\beta=180

αβ

Solución Paso a Paso

Dado que los ángulos alfa y beta están en la misma línea recta y dado que son ángulos adyacentes. Juntos son iguales a 180 grados y la afirmación es verdadera.

Respuesta:

Verdadero

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Partes de un triángulo

¿Qué es la altura de un triángulo y cómo se calcula?

+
La altura de un triángulo es la línea perpendicular que une un vértice con el lado opuesto, formando un ángulo de 90 grados. Se calcula usando el teorema de Pitágoras cuando conoces dos lados del triángulo rectángulo formado por la altura.

¿Cuántas alturas tiene un triángulo?

+
Todo triángulo tiene exactamente tres alturas, una desde cada vértice hacia el lado opuesto. Estas alturas pueden estar dentro del triángulo (triángulos agudos) o fuera de él (triángulos obtusos).

¿Cómo usar la altura para calcular el área de un triángulo?

+
El área de un triángulo se calcula con la fórmula: Área = (base × altura) ÷ 2. La altura debe ser perpendicular a la base elegida para obtener el resultado correcto.

¿Qué diferencia hay entre altura interior y exterior?

+
La altura interior pasa por dentro del triángulo, mientras que la altura exterior requiere extender el lado para formar la perpendicular. En triángulos obtusos, algunas alturas son exteriores.

¿Cómo calcular la altura en un triángulo isósceles?

+
En un triángulo isósceles, la altura desde el vértice superior divide la base en dos partes iguales. Se calcula usando el teorema de Pitágoras con la mitad de la base y uno de los lados iguales.

¿Qué pasos seguir para resolver problemas de altura?

+
1. Identifica qué tipo de triángulo tienes, 2. Localiza los datos conocidos (lados, ángulos), 3. Aplica el teorema de Pitágoras si es necesario, 4. Usa fórmulas de área cuando corresponda, 5. Verifica tu resultado.

¿Cómo se relaciona la altura con el área de paralelogramos?

+
En paralelogramos, la altura es la distancia perpendicular entre dos lados paralelos. El área se calcula multiplicando la base por esta altura: Área = base × altura.

¿Qué errores comunes se cometen al calcular alturas?

+
Los errores más frecuentes incluyen: confundir altura con lado del triángulo, no verificar que la línea sea perpendicular, usar la fórmula incorrecta para el tipo de figura, y no aplicar correctamente el teorema de Pitágoras.

Continúa tu viaje matemático

Domina primero la Partes de un triángulo, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas que se aprenden en secciones posteriores

Suma de los ángulos internos de un triánguloLos lados o aristas de un triánguloÁngulo exterior de un triánguloÁreaTriánguloTipos de triángulosTriángulo obtusoTriángulo equiláteroIdentificación de un triángulo isóscelesTriángulo escalenoTriángulo agudoTriángulo isóscelesÁrea de un triánguloÁrea de un triángulo rectánguloÁrea del triángulo isóscelesÁrea del triángulo escalenoÁrea del triángulo equiláteroÁreas de Polígonos para 7º GradoTriángulo RectánguloMediana en un triánguloCentro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas¿Cómo calculamos el área de figuras complejas?Todos los términos en el cálculo de triángulos¿Cómo calcular el área de un triángulo usando trigonometría?PerímetroPerímetro de un triángulo¿Cómo calculamos el perímetro de los polígonos?

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones
Cálculo de ángulos en cuadriláteros Determinar la medida de los ángulos dados Encontrar la medida de los ángulos en un triángulo ¿Es posible...? Identificación de los lados en un triángulo Identificando los lados en un triángulo usando mediana y altura Identificando y definiendo elementos Identificar el valor mayor Mediana en un triángulo isósceles - propiedades Mediana en un triángulo rectángulo Uso de ángulos en un triángulo Uso de la mediana para calcular el perímetro Uso de las propiedades de la mediana Uso del teorema: la mediana de un triángulo lo divide en dos triángulos de la misma área Uso de rectas paralelas Verdadero / falso