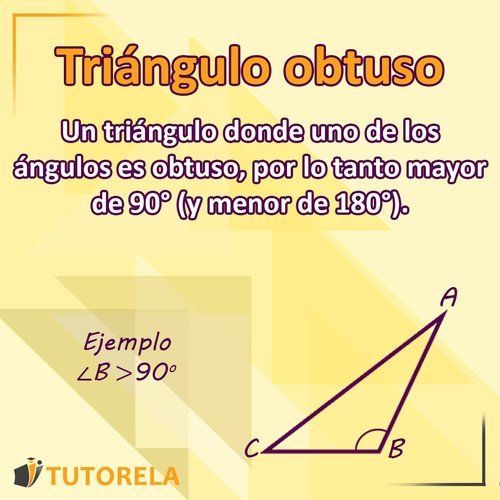
El triángulo obtuso es un triángulo que posee un ángulo obtuso (mayor de grados y menor de grados) y dos ángulos agudos (que cada uno de ellos es inferior a grados). El resultado de la suma de los tres ángulos juntos es grados.
Ejercicios de Triángulos Obtusos - Práctica y Problemas
Practica con ejercicios de triángulos obtusángulos. Aprende a identificar ángulos obtusos, calcular medidas y resolver problemas paso a paso con ejemplos.
📚¿Qué aprenderás practicando con triángulos obtusos?
- Identificar triángulos obtusángulos por sus ángulos mayores a 90°
- Calcular el valor de ángulos obtusos usando la suma de 180°
- Comparar ángulos en triángulos obtusángulos para determinar el mayor
- Resolver ecuaciones con ángulos relacionados algebraicamente
- Clasificar triángulos como obtusos, agudos o rectos usando medidas
- Aplicar el teorema de Pitágoras para identificar tipos de triángulos
Entendiendo la Tipos de triangulos
Explicación completa con ejemplos
Definición de triángulo obtusángulo
Practicar Tipos de triangulos
Pon a prueba tus conocimientos con más de 20 cuestionarios
Dado el triángulo equilátero, halla X
ejemplos con soluciones para Tipos de triangulos
Soluciones paso a paso incluidas
Ejercicio #1
¿Qué triángulo fue dado aquí?
Solución Paso a Paso
Como ninguno de los lados tiene la misma longitud que el otro, es un triángulo escaleno.
Respuesta:
Triángulo escaleno
Solución en video
Ejercicio #2
¿Qué triángulo se da en el dibujo?
Solución Paso a Paso
Como sabemos que los lados AB, BC y CA son todos iguales a 6,
Todos son iguales entre sí y, por lo tanto, el triángulo es equilátero.
Respuesta:
Triángulo equilátero
Solución en video
Ejercicio #3
¿Qué triángulo se da en el dibujo?
Solución Paso a Paso
Como todos los ángulos de un triángulo son menores que 90° y la suma de los ángulos de un triángulo es igual a 180°:
El triángulo es isósceles.
Respuesta:
Triángulo isósceles
Solución en video
Ejercicio #4
Cuál triángulo es el siguiente
Solución Paso a Paso
Dado que en un triángulo obtusángulo basta con que uno de los ángulos sea mayor que 90°, y en el triángulo dado tenemos un ángulo C mayor que 90°,
Además, la suma de los ángulos del triángulo dado es 180 grados:
El triángulo es obtusángulo.
Respuesta:
Triángulo obtusángulo
Solución en video
Ejercicio #5
Cuál es el triángulo dado en el dibujo
Solución Paso a Paso
Dado que los lados AB y AC son ambos iguales a 9, lo que significa que los catetos del triángulo son iguales y la base BC es igual a 5,
Por lo tanto, el triángulo es isósceles.
Respuesta:
Triángulo isósceles
Solución en video
Preguntas Frecuentes
¿Cómo identificar un triángulo obtusángulo?
+Un triángulo obtusángulo tiene un ángulo mayor a 90° y menor a 180°, mientras que los otros dos ángulos son agudos (menores a 90°). La suma de los tres ángulos siempre es 180°.
¿Cuántos ángulos obtusos puede tener un triángulo?
+Un triángulo solo puede tener un ángulo obtuso. Si tuviera dos ángulos mayores a 90°, la suma superaría los 180°, lo cual es imposible en un triángulo.
¿Cómo calcular un ángulo obtuso en un triángulo?
+Para calcular un ángulo obtuso: 1) Suma los dos ángulos agudos conocidos, 2) Resta esta suma de 180°, 3) El resultado es el ángulo obtuso.
¿Qué diferencia hay entre triángulo obtuso y triángulo agudo?
+El triángulo obtuso tiene un ángulo mayor a 90°, mientras que el triángulo agudo tiene todos sus ángulos menores a 90°. Ambos tipos pueden ser escalenos, isósceles, pero nunca equiláteros.
¿Puede un triángulo isósceles ser obtuso?
+Sí, un triángulo isósceles puede ser obtuso cuando el ángulo entre los dos lados iguales es mayor a 90°. En este caso, los dos ángulos de la base serán agudos e iguales.
¿Cómo usar el teorema de Pitágoras para identificar triángulos obtusos?
+En un triángulo con lados a, b, c (donde c es el mayor): Si a² + b² < c², el triángulo es obtuso. Si a² + b² = c², es rectángulo. Si a² + b² > c², es agudo.
¿Cuáles son los errores más comunes al trabajar con triángulos obtusos?
+Los errores más frecuentes incluyen: confundir ángulos obtusos con ángulos reflejos, pensar que un triángulo puede tener dos ángulos obtusos, y no verificar que la suma de ángulos sea 180°.
¿En qué situaciones de la vida real encontramos triángulos obtusos?
+Los triángulos obtusos aparecen en arquitectura (techos inclinados), navegación (triangulación), diseño gráfico, y construcción. También en problemas de optimización donde se necesita maximizar o minimizar áreas.