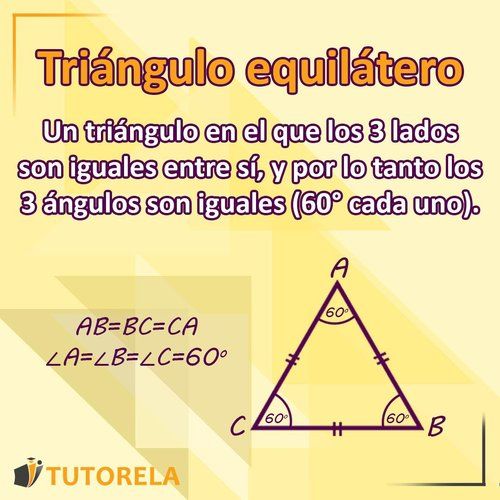
El triángulo equilátero es un triángulo que todos sus lados tienen la misma longitud.
Esto implica también que todos sus ángulos sean iguales, es decir, cada ángulo mide grados (recordemos que la suma de los ángulos de un triángulo es grados y, por lo tanto, estos grados se dividen en partes iguales por los tres ángulos).
Dado un triángulo isósceles:
¿Cuál es su perímetro?
¿Qué triángulo se da en el dibujo?
La medida del ángulo C es de 90°, por lo tanto es un ángulo recto.
Si uno de los ángulos del triángulo es recto, es un triángulo rectángulo.
Respuesta:
Triángulo rectángulo
¿Qué triángulo se da en el dibujo?
Como todos los ángulos de un triángulo son menores que 90° y la suma de los ángulos de un triángulo es igual a 180°:
El triángulo es isósceles.
Respuesta:
Triángulo isósceles
Cuál triángulo es el siguiente
Dado que en un triángulo obtusángulo basta con que uno de los ángulos sea mayor que 90°, y en el triángulo dado tenemos un ángulo C mayor que 90°,
Además, la suma de los ángulos del triángulo dado es 180 grados:
El triángulo es obtusángulo.
Respuesta:
Triángulo obtusángulo
Cuál es el triángulo dado en el dibujo
Dado que los lados AB y AC son ambos iguales a 9, lo que significa que los catetos del triángulo son iguales y la base BC es igual a 5,
Por lo tanto, el triángulo es isósceles.
Respuesta:
Triángulo isósceles
¿Qué triángulo se da en el dibujo?
Como sabemos que los lados AB, BC y CA son todos iguales a 6,
Todos son iguales entre sí y, por lo tanto, el triángulo es equilátero.
Respuesta:
Triángulo equilátero