Ejercicios de Área del Triángulo Isósceles - Práctica
Practica el cálculo del área de triángulos isósceles con ejercicios paso a paso. Domina la fórmula base × altura ÷ 2 y resuelve problemas reales
📚¿Qué aprenderás practicando el área del triángulo isósceles?
- Aplicar la fórmula área = (base × altura) ÷ 2 correctamente
- Identificar la altura, mediana y bisectriz como líneas coincidentes
- Resolver ejercicios con triángulos isósceles rectángulos
- Calcular el área cuando solo conoces la mitad de la base
- Trabajar con medidas en centímetros cuadrados
- Dominar problemas de nivel básico a avanzado paso a paso
Entendiendo la Área del triángulo isósceles
Explicación completa con ejemplos
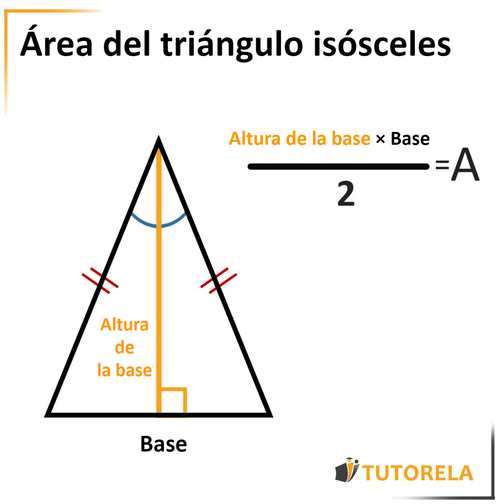
Fórmula para calcular el área del triángulo isósceles

Practicar Área del triángulo isósceles
Pon a prueba tus conocimientos con más de 27 cuestionarios
Calcule el área del triángulo ABC:
Dado que: Perímetro=26
ejemplos con soluciones para Área del triángulo isósceles
Soluciones paso a paso incluidas
Ejercicio #1
Calcula el área del triángulo siguiente:
Solución Paso a Paso
La fórmula de cálculo del área triangular es:
(el lado * la altura del lado que desciende al lado) /2
Es decir:
Ahora reemplazamos los datos existentes:
Respuesta:
10
Solución en video
Ejercicio #2
Calcula el área del triángulo ABC mediante los datos del dibujo:
Solución Paso a Paso
En primer lugar, recordemos la fórmula para el área de un triángulo:
(el lado * la altura del desciende al lado) /2
En la pregunta tenemos tres datos, ¡pero uno de ellos es redundante!
Solo tenemos una altura, la línea que forma un ángulo de 90 grados - AD,
El lado al que desciende la altura es CB,
Por lo tanto, podemos usarlos en nuestro cálculo:
Respuesta:
36 cm²
Solución en video
Ejercicio #3
Calcula el área del triángulo rectángulo a continuación:
Solución Paso a Paso
Como vemos que AB es perpendicular a BC y forma un ángulo de 90 grados
Se puede argumentar que AB es la altura del triángulo.
Entonces podemos calcular el área de la siguiente manera:
Respuesta:
24 cm²
Solución en video
Ejercicio #4
Halla el área del triángulo (tenga en cuenta que esto no siempre es posible)
Solución Paso a Paso
La fórmula para calcular el área de un triángulo es:
(lado * altura correspondiente al lado) / 2
Observa que en el triángulo que se nos proporciona, tenemos la longitud del lado pero no la altura.
Es decir, no tenemos datos suficientes para realizar el cálculo.
Respuesta:
No se puede calcular
Solución en video
Ejercicio #5
Dado el triángulo ABC.
AC = 10 cm, AD = 3 cm, BC = 11.6 cm
¿Cuál es el área del triángulo?
Solución Paso a Paso
El triángulo que estamos viendo es el triángulo grande - ABC
El triángulo está formado por tres lados AB, BC y CA.
Ahora recordemos lo que necesitamos para el cálculo de un área triangular:
(lado x la altura que desciende del lado)/2
Por lo tanto, lo primero que debemos encontrar es una altura y un lado adecuados.
Se nos da el AC lateral, pero no hay altura que desciende, por lo que no nos sirve.
El lado AB no está dado,
Y así nos quedamos con el lado BC, que está dado.
Por el lado BC desciende la altura AD (los dos forman un ángulo de 90 grados).
Se puede argumentar que BC es también una altura, pero si profundizamos parece que CD puede ser una altura en el triángulo ADC,
y BD es una altura en el triángulo ADB (ambos son los lados de un triángulo rectángulo, por lo tanto son la altura y el lado).
Como no sabemos si el triángulo es isósceles o no, tampoco es posible saber si CD=DB, o cuál es su razón, y esta teoría falla.
Recordemos nuevamente la fórmula del área triangular y reemplacemos los datos que tenemos en la fórmula:
(lado* la altura que desciende del lado)/2
Ahora reemplazamos los datos existentes en esta fórmula:
Respuesta:
17.4
Solución en video
Preguntas Frecuentes
¿Cuál es la fórmula para calcular el área de un triángulo isósceles?
+La fórmula es: Área = (base × altura) ÷ 2. Es la misma fórmula que para cualquier triángulo, multiplicando la base por la altura y dividiendo entre dos.
¿Por qué la altura, mediana y bisectriz coinciden en un triángulo isósceles?
+En un triángulo isósceles, la altura desde el vértice opuesto a la base, la mediana y la bisectriz de ese ángulo son la misma línea. Esta es la propiedad principal que facilita los cálculos del área.
¿Cómo calculo el área si solo tengo la mitad de la base?
+Si tienes la mitad de la base, simplemente multiplícala por 2 para obtener la base completa. Por ejemplo, si la mitad es 4 cm, la base total es 8 cm.
¿Qué pasos debo seguir para resolver ejercicios de área del triángulo isósceles?
+1. Identifica la base y la altura del triángulo
2. Si solo tienes la mediana, úsala como altura
3. Aplica la fórmula: (base × altura) ÷ 2
4. Expresa el resultado en unidades cuadradas
¿Cómo resuelvo el área de un triángulo isósceles rectángulo?
+En un triángulo isósceles rectángulo, los dos lados iguales son los catetos. Usa estos catetos como base y altura en la fórmula: Área = (cateto₁ × cateto₂) ÷ 2.
¿Qué errores comunes debo evitar al calcular el área?
+Errores frecuentes incluyen: confundir la mitad de la base con la base completa, no identificar correctamente la altura, y olvidar dividir entre 2 en la fórmula final.
¿En qué unidades se expresa el área de un triángulo?
+El área siempre se expresa en unidades cuadradas. Si las medidas están en centímetros, el área será en cm². Si están en metros, será en m².
¿Puedo usar la mediana como altura en todos los triángulos?
+No, solo en triángulos isósceles la mediana de la base coincide con la altura. En otros tipos de triángulos, la mediana y la altura son líneas diferentes.