Perímetro: cálculo del perímetro de un triángulo
Para calcular el perímetrode un triángulo, todo lo que debes hacer es sumar sus tres lados. Si tienes toda la información necesaria, podrás resolver un problema de este tipo en cuestión de segundos, por ejemplo:
Fórmula del perímetro de un triángulo:
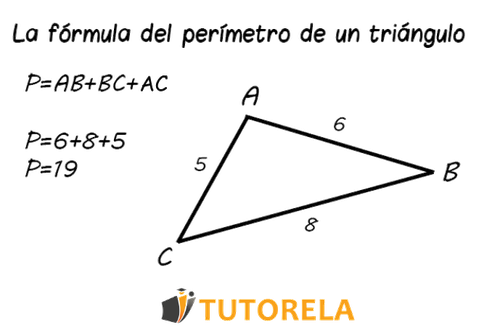
Si nos da un triángulo cuyos lados tienen las siguientes medidas:
En este caso, el perímetro del triángulo, que es la suma de los lados equivaldrá a