Practica ejercicios sobre lados de triángulos, perímetro y clasificación. Resuelve problemas paso a paso con ejemplos detallados y mejora tus habilidades.
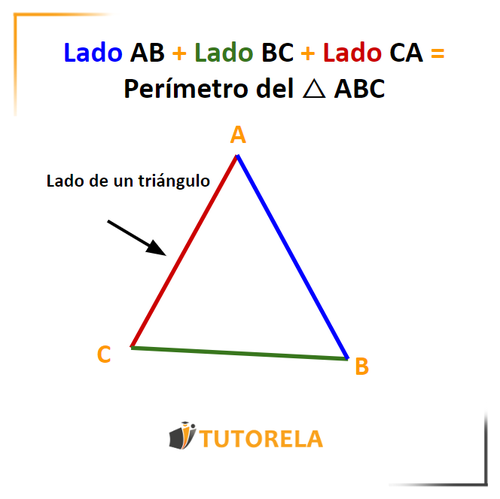
Todo triángulo tiene tres lados. Los lados nos permiten clasificar los diferentes tipos de triángulos, según la medida de estos.
Por ejemplo, un triángulo con dos lados (aristas) iguales es un triángulo isósceles y uno en el que todas sus lados (aristas) son iguales, es un triángulo equilátero. Mientras que un triángulo que tiene todos sus lados diferentes, es un triángulo equilátero.
Marque la respuesta correcta.
AB es el lado del triángulo ABC.
El triángulo ABC isósceles.
Dada: AD mediana.
¿Cuál es el tamaño del ángulo? ?
En un triángulo isósceles, la mediana a la base es también la altura a la base.
Es decir, el lado AD forma un ángulo de 90° con el lado BC.
Es decir, se nos crean dos triángulos rectángulos.
Por lo tanto, el ángulo ADC es igual a 90 grados.
Respuesta:
90
Dado el triángulo siguiente:
Anote cuál es la altura del triángulo ABC.
Una altura en un triángulo es el segmento que une el vértice y el lado opuesto, de tal manera que el segmento forma un ángulo de 90 grados con el lado.
Si observamos el dibujo, podemos notar que el teorema anterior es cierto para la recta AE que cruza BC y forma un ángulo de 90 grados, sale del vértice A y por lo tanto es la altura del triángulo.
Respuesta:
AE
¿Cuál de las siguientes es la altura en el triángulo ABC?
Recordemos la definición de altura:
Una altura es una línea recta que desciende del vértice de un triángulo y forma un ángulo de 90 grados con el lado opuesto.
Por lo tanto, el que forma un ángulo de 90 grados es el lado AB con el lado BC
Respuesta:
AB
Dados los dos triángulos, ¿ EC es un lado en uno de los triángulos?
Cada triángulo tiene 3 lados, repasaremos el triángulo del lado izquierdo:
Sus lados son: AB,BC,CA
Es decir, en este triángulo el lado EC no existe.
Repasemos el triángulo de la derecha:
Sus lados son: ED,EF,FD
Es decir, en este triángulo el lado EC no existe.
Por lo tanto, EC no es un lado en ninguno de los triángulos.
Respuesta:
No
Determinar si la afirmación es verdadera o falsa.
Dado que los ángulos alfa y beta están en la misma línea recta y dado que son ángulos adyacentes. Juntos son iguales a 180 grados y la afirmación es verdadera.
Respuesta:
Verdadero