Número mixto y fracción mayor que 1

En este artículo aprenderemos todo lo necesario sobre los números mixtos y las fracciones mayores de $1$.
Aprenderemos cómo convertir todo a fracción, restar, sumar, multiplicar y comparar. Todo de una forma fácil y eficiente.

Un número mixto es un número compuesto por un número entero y una fracción - de ahí deriva su nombre - combina números enteros y fracciones.
Ejemplos de números mixtos:
$2\frac {3}{5}$, $1\frac {1}{2}$, $4\frac {2}{3}$

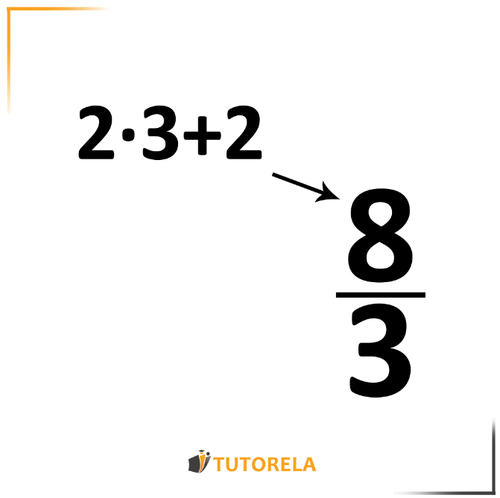
Miremos este número mixto $2\frac {2}{3}$
Para hallar el numerador multiplicamos el número entero por el denominador. Al producto obtenido le sumamos el numerador.
No se modifica nada en el denominador.

Obtendremos:

Primero veamos cómo se ve una fracción que equivale a $1$.
Una fracción que equivale a $1$ es una cuyo numerador y denominador son iguales. Como por ejemplo $2 \over 2$ o $4 \over 4$.
Una fracción mayor que $1$ es una fracción cuyo numerador es más grande que el denominador. 
Siempre que el numerador sea más grande que el denominador la fracción será mayor que $1$. Por ejemplo $3 \over 2$

Observa:

Todo número mixto es mayor que $1$ y podemos escribirlo en forma de una fracción que sea más grande que $1$.

Ejercitación:
Convierte el número mixto $3 \frac {2}{9}$ a una fracción mayor que $1$.
Solución:
Multiplicaremos el entero por el denominador y al producto le añadiremos el numerador. Anotaremos el resultado en el numerador
$3 \times 9+2=29$
El denominador no se verá alterado.
Obtendremos:
$29 \over 3$
Se ve claramente que la fracción obtenida es mayor que $1$ –> el numerador es más grande que el denominador.

En ciertos casos, cuando queramos descubrir la cantidad de unidades o sólo para ordenar el resultado final preferiremos convertir cierta fracción mayor que $1$ a número mixto.

Lo haremos del siguiente modo:
Calcularemos cuántas veces enteras entra el numerador en el denominador - éste será el número entero.
Lo que sobra, lo escribiremos en el numerador y, el denominador quedará intacto (no cambia).
Aprendamos ejercitando:
He aquí una fracción mayor que $1$:
$27 \over 7$
Para convertirla a número mixto dividiremos el numerador por el denominador. Preguntémonos cuántas veces enteras $7$ entra en $27$ ?
Obtendremos:
$27:7=3…….$
3 veces -> éste será el número entero del resultado. 

Ahora veremos cuánto nos queda para completar el numerador $27$.
¿Qué resto hay?
$3 \times 7=21$
$27-21=6$

Tenemos un resto de $6$, eso es lo que se coloca en el numerador.
El resultado final es:
$\frac {27}{7}=3\frac {6}{7}$

Cuando hablamos de suma y resta de fracciones, el primer paso es convertir todo a fracciones (sin números enteros).
De este modo podremos llegar al común denominador para luego sumar o restar los numeradores.

$\frac {5}{2}+1\frac {2}{3}=$
Solución:
Dado este ejercicio de adición con una fracción más grande que $1$ y un número mixto.
El primer paso es convertir el número mixto a fracción del modo que hemos aprendido anteriormente.
Nos dará que:​ $1\frac {2}{3}=\frac {5}{3}$

Volvamos a escribir el ejercicio:

Ahora hallaremos el común denominador multiplicando los denominadores y obtendremos:
$\frac {15}{6}+\frac {10}{6}=\frac {25}{6}$
Podemos convertir el resultado a número mixto así:
$4\frac {1}{6}$

Cuando hablamos de multiplicación y división, por cierto, no hay necesidad de hallar el común denominador, pero sí de convertir los números mixtos en fracciones.
De este modo las operaciones se llevarán a cabo fácilmente.

Comparación entre un número mixto y una fracción mayor que $1$
Para poder comparar entre un número mixto y una fracción mayor que $1$,
Lo primero que deberemos hacer es, claramente, convertir el número mixto a fracción -> es decir fracción con numerador y denominador.
Luego, hallar el común denominador, sólo después de esto podremos comparar los numeradores.

Practiquemos:
Marca el signo correspondiente $<,>,=$
$\frac {23}{36}$_______________$2\frac {5}{7}$

Solución:
Convertiremos el número mixto a fracción y volveremos a escribir el ejercicio.
Obtendremos:

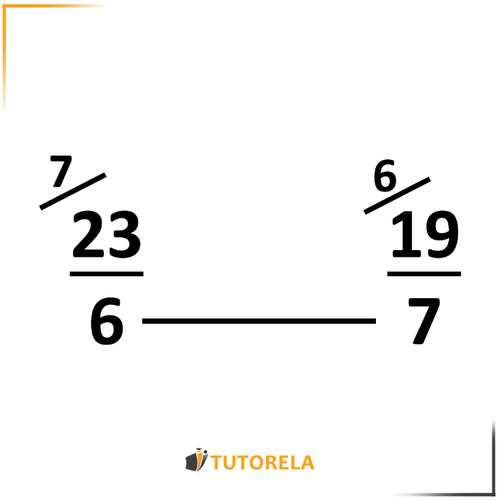
Hallaremos el común denominador multiplicando los denominadores y obtendremos:
$\frac {161}{42}$_______>________$\frac {114}{42}$