La recta real se ve así: una línea horizontal en la que se insertan pequeñas líneas verticales equidistantes.
La recta real o La recta numérica

Características de la recta numérica:
- Debajo de cada línea vertical se inserta un número entero en orden ascendente de izquierda a derecha.
- La distancia entre dos números consecutivos se denomina «segmento».
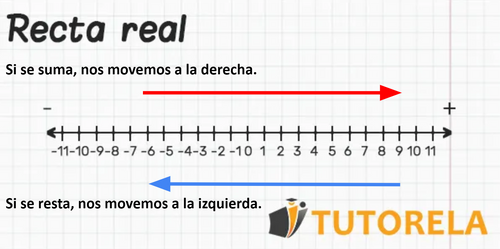
Las operaciones de suma y resta se pueden ver como un movimiento horizontal sobre la recta real.
- Al sumar, nos movemos hacia la derecha.
- Al restar, hacia la izquierda.
¡Pruébate en eje de números!
\( -2 < 0 \)
Para ser más precisos, debemos señalar que la recta numérica es infinita. Por ello, cuando nos referimos a una imagen de la recta real, hacemos referencia a la imagen de una parte de toda la recta.
En la recta real también se pueden representar números decimales, por ejemplo:

Suma y resta en la recta numérica
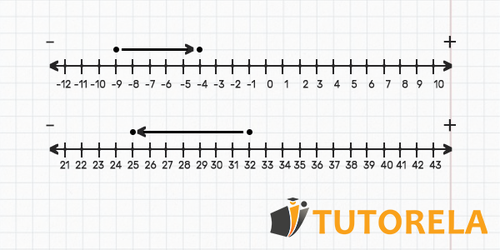
Por ejemplo, veamos los dos ejercicios siguientes que ya están resueltos:
Centrémonos ahora en cada uno de ellos y veámoslos como si fueran un movimiento horizontal sobre la recta real.
- Ejercicio n.º 1:
Empezamos desde , nos movemos segmentos a la derecha y llegamos a . - Ejercicio n.º 2:
Comenzando desde , nos movemos segmentos a la izquierda y llegamos a .
\( -3=-3 \)
Todo numero positivo es mayor que cero
\( 3.98 \) y \( +3.98 \) son dos formas de escribir el mismo número
Ejercicios de práctica con la recta real
Práctica n.º 1
- Dibuja una recta numérica que empiece por y termine en .
- Dibuja una recta numérica que empiece por y termine en .
- Dibuja una recta numérica que empiece por y termine en .
Práctica n.º 2
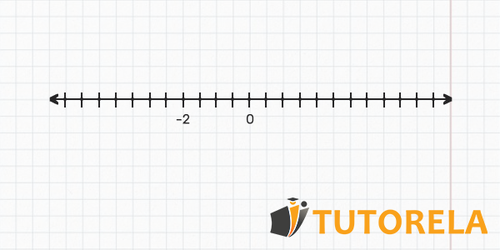
Utilizando la siguiente recta numérica
Señala los siguientes números en ella:
Todos los números negativos aparecen en la recta numérica a la izquierda del número 0
\( 4\frac{1}{2} < -5 \)
\( -4>-3 \)
Práctica n.º 3
- Dibuja una recta numérica que empiece por y termine en . Después, refleja en ella los siguientes ejercicios haciendo uso de puntos y flechas:
Práctica n.º 4
Observa la siguiente recta real y señala si es correcto o no
Si te interesa este artículo también te pueden interesar los siguientes artículos:
Números positivos, negativos y el cero
Eliminación de paréntesis en números reales
Suma y resta de números reales
Multiplicación y división de números reales
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
\( 5 < -5 \)
El signo menos se puede omitir
¿El número \( -6 \) aparece en la recta numérica a la derecha del número \( 2 \)
Ejercicios de la recta real o La recta numérica
Ejercicio 1
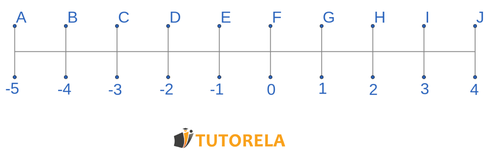
Consigna
¿Cuál es la distancia entre y ?
Solución
Por lo tanto la distancia es salteado
Respuesta
Ejercicio 2
Consigna
¿Qué número aparece en el punto rojo marcado sobre el eje?
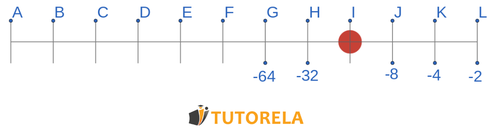
Solución:
Mediante el eje notamos que los saltos entre números están en multiplicar el término anterior por
Por lo tanto
es el punto
Respuesta
El signo siempre se escribe a la izquierda del número
Complete el signo correspondiente
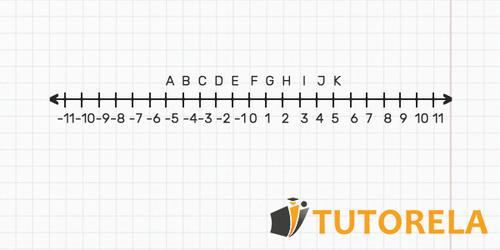
D ? J
¿Cuál es la distancia entre A y K?
Ejercicio 3
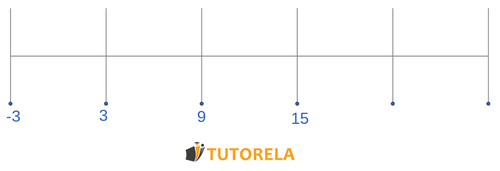
Consigna
Completa los números faltantes
Solución
Notamos que los saltos entre los números están en
Por lo tanto
Respuesta
Ejercicio 4
Consigna
Según el eje:
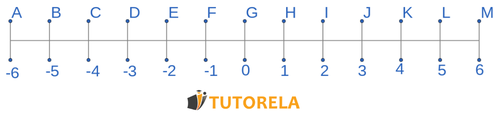
Solución:
Resolvemos el ejercicio
Presta atención que menos multiplicado por menos se convierte en más.
Respuesta
¿Cuál es la distancia entre D y I?
¿Cuál es la distancia entre J y D?
\( -2 < 0 \)
Ejercicio 5
Consigna
Resolver según el eje
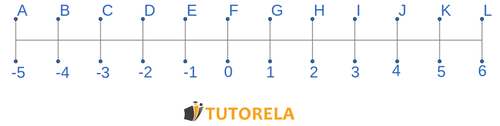
Solución:
Resolver el ejercicio
Presta atención que menos multiplicado por menos se convierte en más.
Respuesta
Preguntas de repaso
¿Qué es la recta numérica y para qué sirve?
La recta numérica o recta real es una línea horizontal dividida en segmentos equidistantes, es decir a la misma distancia uno del otro, la cual sirve para representar números en cada segmento, en la cual se indican números reales.
\( -3=-3 \)
Todo numero positivo es mayor que cero
\( 3.98 \) y \( +3.98 \) son dos formas de escribir el mismo número
¿Cuáles son los elementos de una recta real?
La recta real es una línea horizontal donde se divide por intervalos de la misma distancia, en estos segmentos nos podemos encontrar los siguientes elementos:
- El cero, los positivos y negativos. El cero es un punto donde la recta se divide en dos partes igual, en donde a la derecha nos podemos encontrar a los números positivos y a la izquierda del cero están los negativos.
- Números enteros
- Números racionales
- Números irracionales
¿Por qué se llama recta real?
Se llama recta numérica o recta real, ya que en ella se encuentran a todos los números reales, es decir, al conjunto de números naturales, números enteros, números racionales y números irracionales, todos estos números son un subconjunto de los números reales, en otras palabras son todos los números.
Todos los números negativos aparecen en la recta numérica a la izquierda del número 0
\( 4\frac{1}{2} < -5 \)
\( -4>-3 \)
¿Cuál es la regla numérica para sumar y restar en la recta real?
En la recta numérica vamos a ubicar a los números positivos en la parte derecha del cero y en la parte izquierda a los números negativos, entonces cuando sumamos nos vamos a mover hacia la derecha de la recta, y cuando restamos nos movemos a la izquierda.
Ejemplos de suma y resta en la recta numérica
Ejemplo 1
Consigna. Realiza la siguiente suma en la recta numérica:
Solución: Ubicamos el primer término de la suma en la recta numérica, y como podemos observar es una suma entonces, estamos ubicados en y nos movemos segmentos a la derecha.
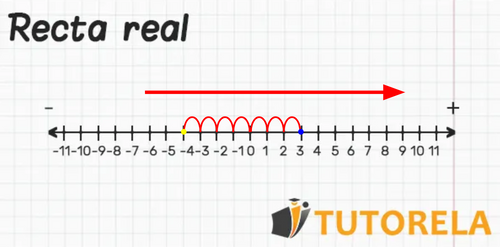
En la recta numérica podemos observar que al recorrer segmentos a la derecha hemos caído en el número , Por lo tanto:
Resultado:
Ejemplo 2
Consigna. Representa la siguiente resta en una recta numérica:
Solución:
Ubicamos el minuendo de la resta en la recta numérica, entonces, empezamos en y después le restamos el sustraendo, es decir, el segundo término de la resta :
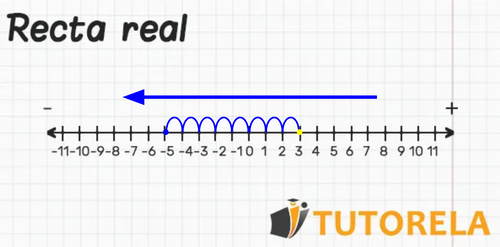
Observamos que hemos caído en el , Usando leyes de signos menos por mas, nos dara menos, por lo tanto esta resta la podemos representrar como:
Por tanto:
Resultado:
\( 5 < -5 \)
El signo menos se puede omitir
¿El número \( -6 \) aparece en la recta numérica a la derecha del número \( 2 \)
ejemplos con soluciones para Eje de números
Ejercicio #1
Solución en video
Solución Paso a Paso
Dado que todo número negativo es necesariamente menor que cero, la respuesta es efectivamente correcta
Respuesta
Verdadero
Ejercicio #2
Solución en video
Solución Paso a Paso
La respuesta es incorrecta porque negativo 3 es mayor que negativo 4:
Respuesta
Falso
Ejercicio #3
¿Cuál es la distancia entre A y K?
Solución en video
Solución Paso a Paso
Es cierto que por haber números en el eje que está hacia el dominio negativo, se puede pensar que el resultado también es negativo.
Pero es importante tener en cuenta que aquí estamos preguntando sobre la distancia.
La distancia nunca puede ser negativa.
Incluso si nos desplazamos hacia o desde el dominio de negatividad, la distancia es un valor existente (valor absoluto).
Podemos pensarlo como si estuviéramos contando el número de pasos, y no importa si comenzamos desde cinco o menos cinco, ambos están a 5 pasos de cero.
Respuesta
10
Ejercicio #4
¿Cuál es la distancia entre F y B?
Solución en video
Solución Paso a Paso
Es cierto que debido a que el desplazamiento en el eje es hacia el dominio negativo, se puede pensar que el resultado también es negativo.
Pero es importante tener en cuenta que aquí estamos preguntando sobre la distancia.
La distancia nunca puede ser negativa.
Incluso si el desplazamiento es hacia el dominio negativo, la distancia es un valor existente.
Respuesta
4
Ejercicio #5
Complete el signo correspondiente
Solución en video
Solución Paso a Paso
Como ambos números son positivos e idénticos, son iguales entre sí:
Respuesta
- Jerarquía de operaciones: suma, resta, multiplicación y división
- Números opuestos
- Eliminación de paréntesis en números reales
- Suma y resta de números reales
- Multiplicación y división de números reales
- Potenciación de números enteros
- Números positivos, negativos y el cero
- La propiedad conmutativa
- Propiedad conmutativa de la suma
- Propiedad conmutativa de la multiplicación
- La propiedad asociativa
- Propiedad asociativa de la suma
- Propiedad asociativa de la multiplicación
- Propiedad distributiva
- La propiedad distributiva para alumnos de 1.º de ESO
- La propiedad distributiva en el caso de las divisiones
- La propiedad distributiva en el caso de la multiplicación
- Las propiedades conmutativas, la multiplicación, la propiedad distributiva y ¡otras más!
- Potencias y raíces
- ¿Qué es una raíz cuadrada?
- Raíz de número negativo
- Potencias y Propiedades de potenciación
- Potencias
- Base de una potencia
- El exponente de una potencia









