Orden o jerarquía de las operaciones con fracciones

Las fracciones no influyen en el orden de las operaciones, por consiguiente, debes tratarlas como a cualquier otro número del ejercicio.

El correcto orden de las operaciones matemáticas es el siguiente:

Explicación completa

Ir a prácticas

¡Pruébate en casos especiales (0 y 1, inverso, linea de fracción)!

¿Cuál es el resultado de la siguiente ecuación?

$36-4\div2$

Quiz y otros ejercicios

Orden o jerarquía de las operaciones con fracciones

El orden de las operaciones matemáticas con fracciones no se diferencia del orden de las operaciones sin fracciones.
Esto significa que, si sabes resolver cierto ejercicio correctamente basándote en el orden de las operaciones matemáticas, también sabrás solucionar un ejercicio con fracciones del mismo modo.
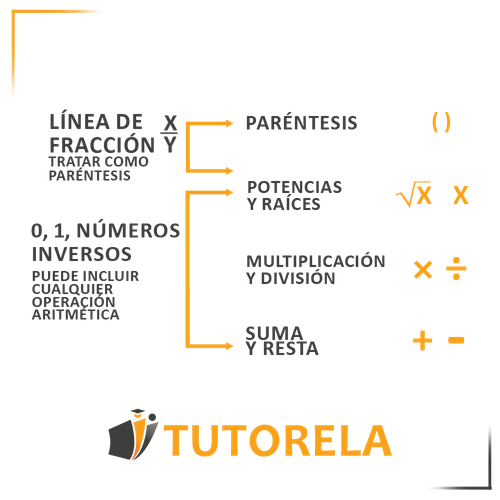
Recordemos el orden de las operaciones:

Paréntesis - Siempre comenzaremos resolviendo lo que haya dentro de los paréntesis, más allá del tipo de operación que sea.
Multiplicaciones y divisiones – El ejercicio se lee de izquierda a derecha. Las multiplicaciones y divisiones tienen la misma jerarquía, por lo tanto, iremos resolviendo acorde al orden de aparición en el ejercicio, de izquierda a derecha.
Sumas y restas - Luego de haber resuelto las operaciones que estaban entre paréntesis y las de multiplicar y dividir seguiremos con las de suma y resta.
Ellas también comparten la misma jerarquía, por lo tanto, iremos resolviendo acorde al orden de aparición en el ejercicio, de izquierda a derecha.

Observa - No hemos dado ninguna importancia a las fracciones, ni las nombramos.
Trataremos a las fracciones como a cualquier otro número, ya sea una fracción común o un número decimal, da lo mismo.

Ejemplos

Ejercicio 1

$3+6 \times \frac{1}{3}=$

Solución:

La multiplicación viene antes de la suma, por lo tanto, primeramente resolveremos todas las multiplicaciones.
Obtendremos:

$3+\frac{6}{3}$
Ahora sumaremos y nos dará:
$3+2=5$

¡Únete a 30,000 estudiantes destacados en matemáticas!

Práctica ilimitada, guía de expertos: mejora tus habilidades matemáticas hoy

Comprueba tu conocimiento

Ejercicio 1

$8\times(5\times1)=$

Ejercicio 2

$7\times1+\frac{1}{2}=$

Ejercicio 3

$\frac{6}{3}\times1=$

Ejercicio 2

$\frac{2}{5} \times (1+3)+4=$

Solución:
Los paréntesis vienen en primer lugar, por lo tanto, comenzaremos resolviendo lo que se encuentra entre ellos.

Obtendremos:
$\frac{2}{5} \times 4+4=$
La multiplicación viene antes de la suma, por lo tanto, seguiremos con la multiplicación.

Obtendremos:
$\frac{8}{5}+4$
Ahora sumaremos y nos dará:

$4\frac{8}{5}=5\frac{3}{5}$

Ejercicio 3

$0.3+(0.4+0.1) \times 4=$

Solución:

Comenzaremos con el ejercicio que está entre paréntesis.

Resolveremos y obtendremos:
$0.3+0.5 \times 4=$

La multiplicación se resuelve antes que la suma, entonces seguiremos con ella.

Obtendremos:

$0.3+2=$

Sumaremos y nos dará:

$0.3+2=2.3$

¿Sabes cuál es la respuesta?

Ejercicio 1

$(3\times5-15\times1)+3-2=$

Ejercicio 2

$(5\times4-10\times2)\times(3-5)=$

Ejercicio 3

$(5+4-3)^2:(5\times2-10\times1)=$

Ejercicio 4

$8-9:18 \times 6+5=$

Solución:

Sabemos que si no hay paréntesis comenzamos con la multiplicación y la división.
Pero ¿en qué orden?
Acorde al orden de aparición en el ejercicio, de izquierda a derecha.
Comenzamos a leer el ejercicio y nos topamos con una división, por lo tanto, comenzaremos con ella.

Obtendremos:

$8-\frac{9}{18} \times 6+5=$

Seguiremos con la multiplicación. Nos percataremos de que $9 \over 18$ es, de hecho, $1 \over 2$
Obtendremos:
$8-\frac{1}{2} \times 6+5=$

$8-3+5=$

Ahora continuaremos con las operaciones de suma y resta según el orden de aparición.
Cuando comenzamos a leer el ejercicio desde el principio nos topamos con una resta, por consiguiente, la resolveremos en primer lugar. Obtendremos:

$5+5=10$

Ejercicio 5

$5 \times 3-\frac{4}{8} \times 2-3=$

Solución:

No hay paréntesis así que comenzaremos con las operaciones de multiplicación y división acorde a su orden de aparición en el ejercicio.
Comenzaremos con la primera multiplicación de la izquierda.

Obtendremos:

$15-\frac{4}{8} \times 2-3=$

Continuaremos con la siguiente multiplicación y obtendremos:

$15-\frac{8}{8}-3=$

Nos percataremos de que $8 \over 8$ es $1$ .

Restaremos de izquierda a derecha según el orden de aparición y obtendremos:

$15-1-3=$

$14-3=11$

Comprueba que lo has entendido

Ejercicio 1

$$ 100+5-100+5 $$

Ejercicio 2

Resuelva el ejercicio

$$ 3-4+2+1 $$

Ejercicio 3

Resuelva el ejercicio

$$ 9-3+4-2 $$

ejemplos con soluciones para Casos especiales (0 y 1, inverso, linea de fracción)

Ejercicio #1

$8\times(5\times1)=$

Solución en video

Solución Paso a Paso

Según el orden de las operaciones, primero resolvemos la expresión entre paréntesis:

$5\times1=5$

Ahora multiplicamos:

$8\times5=40$

Respuesta

Ejercicio #2

$(3\times5-15\times1)+3-2=$

Solución en video

Solución Paso a Paso

La simplificación de esta expresión se basa en el orden de operaciones que indica que la potenciación tiene prioridad sobre la multiplicación y división, las cuales tienen prioridad sobre la suma y resta, y que las operaciones de igual prioridad se resuelven de izquierda a derecha,

siguiendo la simplificación básica, la multiplicación se realiza antes que la división y la suma, por lo tanto, primero calculamos los valores de las multiplicaciones y luego realizamos las operaciones de división y resta

$3\cdot5-15\cdot1+3-2= \\ 15-15+3-2= \\ 1$ Por lo tanto, la respuesta correcta es respuesta b'.

Respuesta

$1$

Ejercicio #3

$(5\times4-10\times2)\times(3-5)=$

Solución en video

Solución Paso a Paso

La simplificación de esta expresión dentro del paréntesis sigue el orden de operaciones que indica que la multiplicación y división se realizan antes que la suma y resta, y si hay paréntesis, estos tienen prioridad sobre todo,

en la simplificación dada se establece una multiplicación entre dos pares de términos, por lo tanto simplificamos los términos que están dentro de cada par de términos por separado,

Comenzamos simplificando el término que está dentro del paréntesis izquierdo, esto se hace de acuerdo al orden de operaciones mencionado, dado que la multiplicación se realiza antes que la resta, se realiza primero la multiplicación en este término y luego se lleva a cabo la operación de resta en los términos de este, en contraste simplificamos el término que está en el paréntesis derecho y se lleva a cabo la operación de resta en él:

$(5\cdot4-10\cdot2)\cdot(3-5)= \\ (20-20)\cdot(-2)= \\ 0\cdot(-2)=\\$ Nos queda si así realizamos la última multiplicación que se indica, es la multiplicación que se realiza entre los términos dentro de los paréntesis en el término original, se realiza mientras recordamos que multiplicar cualquier número por 0 dará como resultado 0:

$0\cdot(-2)=\\ 0$ Por lo tanto, la respuesta correcta es la respuesta d'.

Respuesta

$0$

Ejercicio #4

$(5+4-3)^2:(5\times2-10\times1)=$

Solución en video

Solución Paso a Paso

Este concepto básico es la jerarquía de las operaciones, que establece que la multiplicación y la división se realizan antes que la suma y la resta, y que las operaciones dentro de los paréntesis tienen prioridad sobre todas ellas,

en este contexto se establece una división entre dos números negativos, notemos que los negativos a la izquierda indican una fortaleza, por lo tanto, al seguir la jerarquía de las operaciones mencionada anteriormente, primero simplificaremos la división que está dentro de los paréntesis, y a medida que avanzamos obtendremos el resultado que se deriva de simplificar la división que está dentro de los paréntesis con fortaleza dada y en el paso final dividiremos el resultado que se obtiene del resultado de simplificar la división que está dentro de los paréntesis,

Si seguimos este proceso en la división que está dentro de los paréntesis a la izquierda, donde realizamos las operaciones de multiplicación y división, a medida que avanzamos en fortaleza, a diferencia de simplificar la división que está dentro de los paréntesis a la derecha, esto resulta en seguir la jerarquía de las operaciones mencionada, dado que la multiplicación tiene prioridad sobre la división, primero realizaremos las operaciones de multiplicación que están dentro de los paréntesis y a medida que avanzamos realizaremos la operación de división:

$(5+4-3)^2:(5\cdot2-10\cdot1)= \\ (-2)^2:(10-10)= \\ 4:0\\$ Destacamos quela razón por la cual el resultado de las operaciones que están dentro de la división a la izquierda es positivo, este resultado lo llevamos a los paréntesis, estos los elevamos al paso siguiente en fortaleza, esto es importante recordar quela elevación de cualquier número (positivo o negativo) en fortaleza par da como resultado un número positivo,

Por lo tanto, en la última división que recibimos de establecer una operación de división en el número 0, esta operación es conocida comouna operación matemática indefinida (y esa es la razón simple por la cual no se divide nunca un número entre 0) por lo tanto, la división dada da como resultadoun valor que no está definido, comúnmente se denota este valor como"conjunto vacío" y se usa el símbolo :

$\{\empty\}$ En conclusión:

$4:0=\\ \{\empty\}$ Por lo tanto, la respuesta correcta es la respuesta A.

Respuesta

No hay solución

Ejercicio #5

$100+5-100+5$

Solución en video

Solución Paso a Paso

$100+5-100+5=105-100+5=5+5=10$

Respuesta

Ir a prácticas