En artículos previos hemos estudiado sobre números reales y la agrupación de términos, como también sobre el orden de las operaciones matemáticas con paréntesis. En este artículo avanzamos y combinamos los temas a fin de entender cuándo y cómo podemos eliminar los paréntesis en los números reales.
Eliminación de paréntesis en números reales
¿Qué significa la eliminación de paréntesis en números reales?
Cuando hacemos agrupación de términos («suma y resta») en números reales nosotros limitamos el número real dentro de los paréntesis.
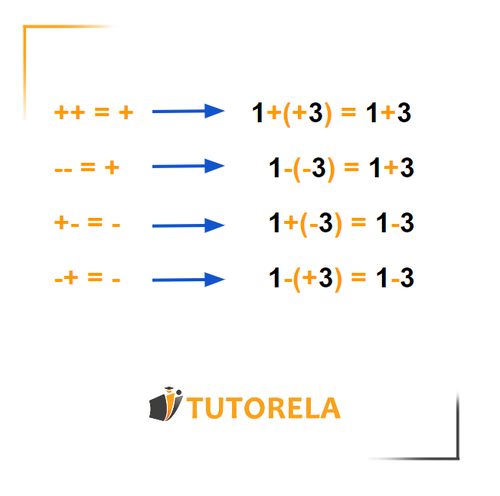
Se pueden quitar los paréntesis pero al eliminarlos se deben recordar las siguientes reglas:
¡Pruébate en características básicas!
¿Cuál es el número opuesto de \( 5 \)
La lógica en este caso es que, el signo de restar nos permite obtener el número opuesto al que se nos ha dado.
Por consiguiente:
- «Menos menos seis» es igual a «más seis», es decir, «seis».
- Del mismo modo, «menos más seis» es igual a «menos seis».
Sin embargo, el signo más no indica una modificación en el número.
Por lo tanto,
- «más menos seis» es igual a «menos seis»
- y «más más seis» es igual a «más seis», es decir, «seis».
Ejemplos:
Observemos nuevamente los tres ejercicios resueltos previamente, ahora los anotaremos sin paréntesis.
Como seguramente recordamos de la clase «números reales», cuando hay un número sin ningún signo entendemos que es positivo.
Por lo tanto,
- en el primer ejercicio podemos escribir «50» y «30» en lugar de «+50» y «+30».
- En cambio, no podemos eliminar el signo más en el tercer ejercicio: en «+4».
Recuerda: Sólo podemos omitir el signo más si el número es el primero de la secuencia.
Cuando resolvemos ejercicios con números reales, en una primera fase tenemos que hacer simplificación de paréntesis según las reglas matemáticas.
Ejemplo:
Ejercicios de eliminación de paréntesis en números reales
Ejercicio 1
Completa:
- __
- __
- __
- __
- __
- __
- -__
¿Cuál es el número opuesto de \( 87 \)
¿Cuál es el número opuesto de \( -7 \)
¿Cuál es el número opuesto de \( -0.25 \)
Ejercicio 2
Resuelve los siguientes ejercicios, antes que nada, haz la reducción de paréntesis:
Ejercicio 3
Consigna
Marcar la respuesta correcta
Solución
Resolvemos los ejercicios entre paréntesis según el orden de las operaciones aritméticas
Continuamos resolviendo los ejercicios entre paréntesis en consecuencia.
Respuesta
¿Cuál es el número opuesto de \( 0.7 \)
¿Cuál es el número opuesto de \( -\frac{8}{7} \)
\( (+0.5)+(+\frac{1}{2})= \)
Ejercicio 4
Consigna
Solución
Primero resolvemos los ejercicios haciendo la eliminación de paréntesis según las leyes de suma y resta
Ordenamos el ejercicio de multiplicación que obtenemos para que nos sea más fácil resolverlo.
Resolvemos el ejercicio de izquierda a derecha
Respuesta
Ejercicio 5
Consigna
Solución
Primero resolvemos los ejercicios reduciendo los paréntesis según las leyes de suma y resta
Prestar atención que obtuvimos un ejercicio de multiplicación con el número y primero lo resolvemos para facilitar el cálculo.
Respuesta
\( (+2.16)+(-4\frac{1}{16})= \)
\( (+\frac{18}{6})-(-\frac{1}{4})= \)
\( (+43)-(+15)= \)
Ejercicio 6
Consigna
Solución
Primero resolvemos los ejercicios eliminando los paréntesis según las leyes de suma y resta
Resolvemos el ejercicio de izquierda a derecha
Respuesta
Ejercicio 7
Consigna
Solución
Multiplicamos el primer elemento entre paréntesis por los elementos del segundo paréntesis
Después multiplicamos el segundo elemento entre paréntesis primarios por los elementos del segundo paréntesis
Resolvemos todos los ejercicios de multiplicación de izquierda a derecha
Ahora sumamos de izquierda a derecha
Respuesta
Si te interesa este artículo también te pueden interesar los siguientes artículos:
Números positivos, negativos y el cero
Eliminación de paréntesis en números reales
Multiplicación y división de números reales
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
\( (-\frac{2}{4})-(+3.5)= \)
\( (-3\frac{2}{6})+(-2.75)= \)
\( (+71)+(-18)= \)
ejemplos con soluciones para Características básicas
Ejercicio #1
¿Cuál es el número opuesto de
Solución en video
Respuesta
Ejercicio #2
¿Cuál es el número opuesto de
Solución en video
Respuesta
Ejercicio #3
¿Cuál es el número opuesto de
Solución en video
Respuesta
Ejercicio #4
¿Cuál es el número opuesto de
Solución en video
Respuesta
Ejercicio #5
¿Cuál es el número opuesto de
Solución en video
Respuesta
- Jerarquía de operaciones: suma, resta, multiplicación y división
- Suma y resta de números reales
- Multiplicación y división de números reales
- Potenciación de números enteros
- Números positivos, negativos y el cero
- La recta real o La recta numérica
- La propiedad conmutativa
- Propiedad conmutativa de la suma
- Propiedad conmutativa de la multiplicación
- La propiedad asociativa
- Propiedad asociativa de la suma
- Propiedad asociativa de la multiplicación
- Propiedad distributiva
- La propiedad distributiva para alumnos de 1.º de ESO
- La propiedad distributiva en el caso de las divisiones
- La propiedad distributiva en el caso de la multiplicación
- Las propiedades conmutativas, la multiplicación, la propiedad distributiva y ¡otras más!
- Potencias y raíces
- ¿Qué es una raíz cuadrada?
- Raíz de número negativo
- Potencias y Propiedades de potenciación
- Potencias
- Base de una potencia
- El exponente de una potencia









