Preguntas Frecuentes
Todo lo que necesitas saber Razón de cambio de una función
¿Qué es la tasa de variación de una función?
+ La tasa de variación describe el ritmo en que cambian las variables Y respecto al cambio de las variables X. En funciones lineales, la tasa de variación es constante y equivale a la pendiente de la recta.
¿Cómo saber si una función tiene tasa de variación constante?
+ Una función tiene tasa de variación constante si: 1) Su gráfica es una línea recta, 2) En una tabla de valores, Y cambia siempre en la misma cantidad cuando X aumenta en intervalos fijos, 3) Los peldaños trazados en la gráfica tienen la misma altura.
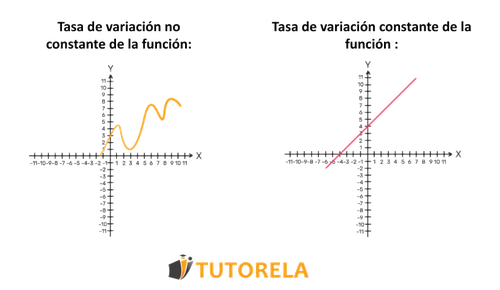
¿Cuál es la diferencia entre tasa de variación constante e inconstante?
+ Tasa constante: intervalos fijos de X producen intervalos fijos de Y (función lineal). Tasa inconstante: intervalos fijos de X producen intervalos diferentes de Y (función no lineal con pendiente variable).
¿Cómo calcular la tasa de variación usando una tabla de valores?
+ Para calcular la tasa de variación: 1) Elige intervalos fijos para X (ejemplo: 1,2,3,4), 2) Calcula los valores correspondientes de Y, 3) Observa si Y cambia constantemente, 4) La tasa será el cambio en Y dividido entre el cambio en X.
¿Qué son los peldaños en una gráfica de función?
+ Los peldaños son marcas que parecen escalones trazados sobre la gráfica. La base representa el intervalo entre variables X y la altura representa el intervalo entre variables Y, ayudando a visualizar la tasa de variación.
¿Por qué es importante estudiar la tasa de variación?
+ La tasa de variación ayuda a: entender cómo se relacionan las variables, predecir comportamientos futuros, resolver problemas de la vida real como velocidad y crecimiento, y analizar patrones en datos matemáticos.
¿Cómo identificar tasa de variación inconstante en una gráfica?
+ Una gráfica muestra tasa inconstante cuando: la línea no es recta (curva, parábola, etc.), la pendiente cambia en diferentes segmentos, y los peldaños trazados tienen alturas diferentes para bases iguales.
¿Qué ejemplos de la vida real usan tasa de variación?
+ Ejemplos comunes incluyen: velocidad constante vs aceleración (movimiento), crecimiento poblacional, temperatura a lo largo del día, ganancias empresariales, y consumo de combustible en vehículos.