Ejercicios de Tasa de Variación de una Función Gráfica

Entendiendo la Tasa de variación de una función representada gráficamente

Explicación completa con ejemplos

Tasa de variación de una función representada gráficamente

La tasa de variación de una función representada gráficamente nos permite determinar de un modo mucho más intuitivo si se trata de un ritmo constante (fijo) o inconstante (que no es fijo), y también si se trata de un ritmo más rápido (pendiente más inclinada) o más lento (pendiente más moderada).

La siguiente gráfica puede demostrar lo mencionado anteriormente de la mejor manera:

Tasa de variación de una función representada gráficamente

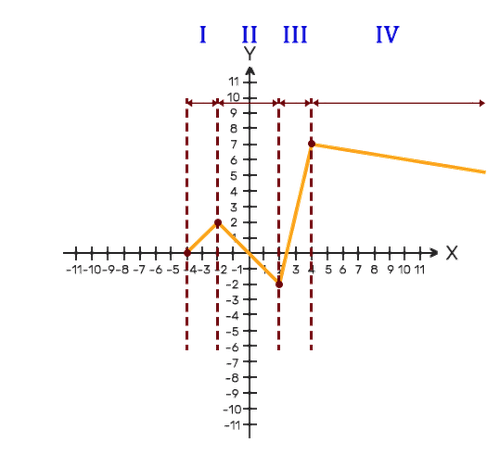
Observemos la gráfica. Nos percataremos de que está dividida en 4 ramas diferentes. Ahora analizaremos cada una de las ramas:

Rama 1: el gráfico sube (función creciente) a ritmo constante (línea recta).
Rama 2: El gráfico baja (función decreciente) a ritmo constante (línea recta).
Rama 3: el gráfico sube (función creciente) a ritmo constante (línea recta) y más rápidamente que el de la rama 1 (la pendiente es más inclinada).
Rama 4: El gráfico baja (función decreciente) a ritmo constante (línea recta) y más lentamente que el de la rama 2 (la pendiente es más moderada).

Explicación completa

Practicar Tasa de variación de una función representada gráficamente

Pon a prueba tus conocimientos con más de 9 cuestionarios

Dada una tabla que muestra puntos en el borde de la función, determine si la tasa de cambio es uniforme o no.

ejemplos con soluciones para Tasa de variación de una función representada gráficamente

Soluciones paso a paso incluidas

Ejercicio #1

Dada la siguiente gráfica, determine si la tasa de cambio es uniforme o no

Solución Paso a Paso

Respuesta:

Uniforme

Solución en video

Ejercicio #2

Dada la siguiente gráfica, determine si la tasa de cambio es uniforme o no

Solución Paso a Paso

Respuesta:

La gráfica no representa la función

Solución en video

Ejercicio #3

Dada la siguiente gráfica, determine si la tasa de cambio es uniforme o no

Solución Paso a Paso

Respuesta:

La gráfica no representa la función

Solución en video

Ejercicio #4

Dada la siguiente gráfica, determine si la tasa de cambio es uniforme o no

Solución Paso a Paso

Respuesta:

No uniforme

Solución en video

Ejercicio #5

Dada la siguiente gráfica, determine si la tasa de cambio es uniforme o no

Solución Paso a Paso

Respuesta:

No uniforme

Solución en video

Preguntas Frecuentes

Todo lo que necesitas saber Tasa de variación de una función representada gráficamente

¿Cómo identificar una tasa de variación constante en una gráfica?

+

Una función tiene tasa de variación constante cuando su gráfica forma una línea recta. La pendiente (inclinación) permanece igual en todos los puntos de la función, lo que significa que el cambio es uniforme.

¿Qué diferencia hay entre función creciente y decreciente en la gráfica?

+

Una función creciente tiene pendiente positiva (la línea sube de izquierda a derecha), mientras que una función decreciente tiene pendiente negativa (la línea baja de izquierda a derecha).

¿Cómo se ve una función con tasa de variación inconstante?

+

Se representa mediante una línea curva en lugar de una línea recta. La pendiente cambia constantemente, por lo que la velocidad de cambio no es uniforme en toda la función.

¿Qué significa que una pendiente sea más inclinada en la gráfica?

+

Una pendiente más inclinada indica una tasa de variación más rápida. Esto significa que la función cambia más rápidamente, ya sea creciendo o decreciendo con mayor velocidad.

¿Cómo analizar múltiples ramas en una gráfica de función?

+

Cada rama se analiza por separado observando: 1) Si sube o baja (creciente/decreciente), 2) Si es línea recta o curva (constante/inconstante), 3) La inclinación para determinar la velocidad de cambio.

¿Qué indica el coeficiente de X en la tasa de variación?

+

El coeficiente de X representa la pendiente de la función. Si es positivo, la función es creciente; si es negativo, es decreciente. Su valor absoluto indica qué tan rápido cambia la función.

¿Cómo encontrar los puntos de intersección con los ejes?

+

Para el eje Y: sustituir X=0 en la función. Para el eje X: sustituir y=0 y resolver para X. Estos puntos ayudan a dibujar y entender mejor la gráfica de la función.

¿Por qué es importante analizar la tasa de variación gráficamente?

+

El análisis gráfico permite una comprensión intuitiva y visual del comportamiento de la función, facilitando identificar patrones, tendencias y cambios en la velocidad de crecimiento o decrecimiento.

Continúa tu viaje matemático

Domina primero la Tasa de variación de una función representada gráficamente, luego avanza a estos temas relacionados que construyen sobre tus habilidades con fracciones

Temas sugeridos para practicar con anticipación

Temas que se aprenden en secciones posteriores

Tasa de variación de una función Variación de una función Tasa de variación representada con peldaños en la gráfica de la función Tasa de variación constante Tasa de variación inconstante Tasa de variación de una función representada por una tabla de valores Funciones para séptimo grado Intervalos de crecimiento y de decrecimiento de una función Función creciente Función decreciente Función constante Intervalo de decrecimiento de la función Intervalos de función creciente Dominio de una función Función indefinida Asignación de valor numérico en una función

Practica por Tipo de Pregunta

Elige tu estilo de aprendizaje y formato de práctica preferido para problemas de fracciones

Calcular la tasa de cambio a partir de una ecuación Calcular la tasa de cambio a partir de una tabla Calcular la tasa de cambio en un gráfico