Una función puede ser definida para todos los valores (es decir para toda ). Un ejemplo de este tipo de función es el polinomio - al que estudiaremos en los próximos años.
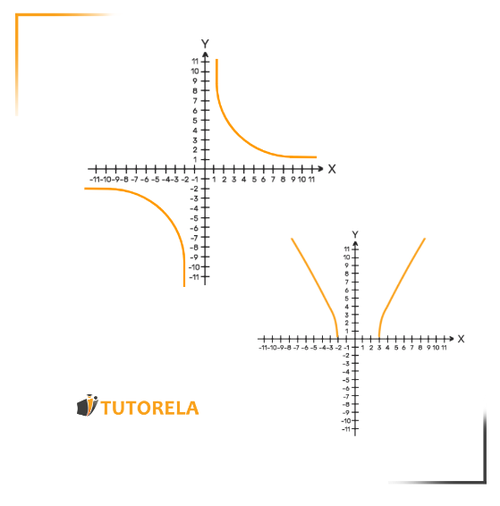
Sin embargo, hay funciones que no están definidas para todos los valores (toda ), ya que si colocamos cierta o cierto rango de valores de recibiremos una expresión considerada «inválida» en matemática. Los valores de para los cuales la función es indefinida causan la discontinuidad de una función.
\( \frac{6}{x+5}=1 \)
¿Cuál es el campo de aplicación de la ecuación?
\( \frac{x+y:3}{2x+6}=4 \)
¿Cuál es el campo de aplicación de la ecuación?
\( \frac{3x:4}{y+6}=6 \)
¿Cuál es el campo de aplicación de la ecuación?
\( 22(\frac{2}{x}-1)=30 \)
¿Cuál es el dominio del ejercicio?
\( 2x+\frac{6}{x}=18 \)
¿Cuál es el dominio del ejercicio?
¿Cuál es el campo de aplicación de la ecuación?
¿Cuál es el campo de aplicación de la ecuación?
¿Cuál es el campo de aplicación de la ecuación?
¿Cuál es el dominio del ejercicio?
x≠0
¿Cuál es el dominio del ejercicio?
x≠0
\( 2x-3=\frac{4}{x} \)
¿Cuál es el dominio del ejercicio?
¿Cuál es el dominio del ejercicio?
\( \frac{5x+8}{2x-6}=30 \)
Dada la siguiente función:
\( \frac{20}{10x-5} \)
¿Cuál es el dominio de la función?
Dada la siguiente función:
\( \frac{2x+2}{3x-1} \)
¿Cuál es el dominio de la función?
Dada la siguiente función:
\( \frac{3x+4}{2x-1} \)
¿Cuál es el dominio de la función?
¿Cuál es el dominio del ejercicio?
x≠0
¿Cuál es el dominio del ejercicio?
x≠3
Dada la siguiente función:
¿Cuál es el dominio de la función?
Dada la siguiente función:
¿Cuál es el dominio de la función?
Dada la siguiente función:
¿Cuál es el dominio de la función?
Dada la siguiente función:
\( \frac{10x-3}{5x-3} \)
¿Cuál es el dominio de la función?
Dada la siguiente función:
\( \frac{2x+2}{9x+6} \)
¿Cuál es el dominio de la función?
Dada la siguiente función:
\( \frac{12}{8x-4} \)
¿Cuál es el dominio de la función?
Dada la siguiente función:
\( \frac{1}{5x-4} \)
¿Cuál es el dominio de la función?
Dada la siguiente función:
\( \frac{24}{21x-7} \)
¿Cuál es el dominio de la función?
Dada la siguiente función:
¿Cuál es el dominio de la función?
Dada la siguiente función:
¿Cuál es el dominio de la función?
Dada la siguiente función:
¿Cuál es el dominio de la función?
Dada la siguiente función:
¿Cuál es el dominio de la función?
Dada la siguiente función:
¿Cuál es el dominio de la función?