Hay una amplia variedad de formas geométricas, sobre las cuales puedes leer en detalle:
Ejercicios de Triángulos - Práctica y Problemas Resueltos
Domina los triángulos con ejercicios prácticos: equiláteros, isósceles, rectángulos y escalenos. Aprende propiedades, ángulos y clasificación paso a paso.
📚¡Practica y Domina Todos los Tipos de Triángulos!
- Identifica y clasifica triángulos equiláteros, isósceles, rectángulos y escalenos
- Calcula ángulos internos aplicando la suma de 180 grados
- Resuelve problemas con el teorema de Pitágoras en triángulos rectángulos
- Determina alturas, medianas y bisectrices en diferentes tipos de triángulos
- Aplica propiedades específicas de cada tipo de triángulo en ejercicios prácticos
- Reconoce características distintivas: lados iguales, ángulos base y hipotenusa
Entendiendo la Triángulo
Explicación completa con ejemplos
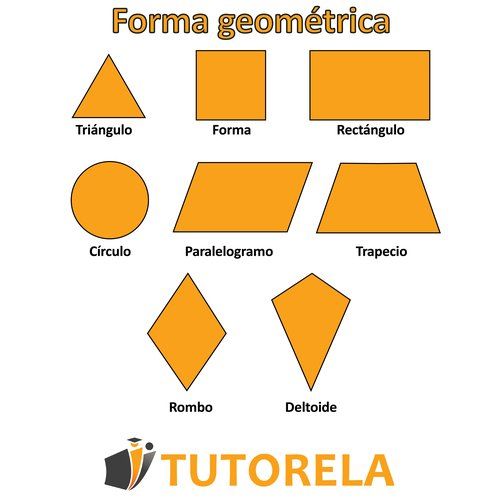
Formas geométricas
Triángulo
Rectángulo
Trapezoide
Paralelogramo
Deltoide
Rombo
Practicar Triángulo
Pon a prueba tus conocimientos con más de 48 cuestionarios
Dado el trapecio de la figura
Dado que la base larga es mayor por 1.5 que la corta
Halla el perímetro del trapecio
ejemplos con soluciones para Triángulo
Soluciones paso a paso incluidas
Ejercicio #1
Dados los tres ángulos:
Ángulo A es igual a 56°
Ángulo B es igual a 89°
Ángulo C es igual a 17°
¿Estos ángulos pueden componer un triángulo?
Solución Paso a Paso
Sumamos los tres ángulos para ver si son iguales a 180 grados:
La suma de los ángulos dados no es igual a 180, por lo que no pueden formar un triángulo.
Respuesta:
No
Solución en video
Ejercicio #2
Dados los tres ángulos:
Ángulo A es igual a 90°
Ángulo B es igual a 115°
Ángulo C es igual a 35°
¿Estos ángulos pueden componer un triángulo?
Solución Paso a Paso
Sumamos los tres ángulos para ver si son iguales a 180 grados:
La suma de los ángulos dados no es igual a 180, por lo que no pueden formar un triángulo.
Respuesta:
No
Solución en video
Ejercicio #3
Dados los tres ángulos:
Ángulo A es igual a 30°
Ángulo B es igual a 60°
Ángulo C es igual a 90°
¿Estos ángulos pueden componer un triángulo?
Solución Paso a Paso
Sumamos los tres ángulos para ver si son iguales a 180 grados:
La suma de los ángulos es igual a 180, por lo que pueden formar un triángulo.
Respuesta:
Si
Solución en video
Ejercicio #4
Dado el rectángulo ABCD que tiene el lado AB de largo 6 cm y el lado BC de largo 4 cm.
¿Cuál es el área del rectángulo?
Solución Paso a Paso
Recuerda que la fórmula para el área de un rectángulo es ancho por alto
Se nos da que la ancho del rectángulo es 6
y que el largo del rectángulo es 4
Por lo tanto calculamos:
6*4=24
Respuesta:
24 cm²
Solución en video
Ejercicio #5
Dado el rombo del dibujo:
¿Cuál es el área?
Solución Paso a Paso
Recordemos que el rombo tiene dos maneras de calcular su área:
La primera es lado por la altura del lado.
La segunda es diagonal por diagonal dividido 2.
Como nos dan las dos diagonales, lo calculamos de la segunda manera:
Respuesta:
14
Solución en video
Preguntas Frecuentes
¿Cuáles son los 4 tipos principales de triángulos?
+Los 4 tipos principales son: triángulo equilátero (3 lados iguales), triángulo isósceles (2 lados iguales), triángulo rectángulo (un ángulo de 90°) y triángulo escaleno (todos los lados diferentes). Cada tipo tiene propiedades únicas que los distinguen.
¿Cómo calcular los ángulos de un triángulo?
+La suma de todos los ángulos internos de cualquier triángulo siempre es 180°. Si conoces dos ángulos, puedes encontrar el tercero restando: Ángulo desconocido = 180° - (ángulo 1 + ángulo 2). Esta regla funciona para todos los tipos de triángulos.
¿Qué es un triángulo equilátero y cuáles son sus propiedades?
+Un triángulo equilátero tiene los 3 lados iguales y los 3 ángulos iguales a 60°. Sus propiedades especiales incluyen:
• Cada altura es también mediana y bisectriz
• Todas las alturas, medianas y bisectrices son iguales
• Es simétrico respecto a sus 3 alturas
¿Cómo identificar un triángulo isósceles?
+Un triángulo isósceles tiene exactamente 2 lados iguales y 2 ángulos base iguales. Para identificarlo: mide los lados y busca dos medidas iguales, o verifica que dos ángulos sean iguales. La mediana a la base también es altura y bisectriz del ángulo del vértice.
¿Qué es la hipotenusa en un triángulo rectángulo?
+La hipotenusa es el lado más largo de un triángulo rectángulo, ubicado opuesto al ángulo de 90°. Los otros dos lados se llaman catetos. La hipotenusa siempre es mayor que cualquiera de los catetos y se calcula usando el teorema de Pitágoras: h² = a² + b².
¿Cuál es la diferencia entre altura, mediana y bisectriz?
+• Altura: línea perpendicular desde un vértice al lado opuesto
• Mediana: línea desde un vértice al punto medio del lado opuesto
• Bisectriz: línea que divide un ángulo en dos partes iguales
En triángulos equiláteros, estas tres líneas coinciden para cada vértice.
¿Cómo resolver problemas de triángulos paso a paso?
+1. Identifica el tipo de triángulo según sus lados y ángulos
2. Anota los datos conocidos (lados, ángulos)
3. Aplica las propiedades específicas del tipo de triángulo
4. Usa fórmulas apropiadas (suma de ángulos = 180°, teorema de Pitágoras)
5. Verifica que tu respuesta tenga sentido geométricamente
¿Cuándo usar el teorema de Pitágoras en triángulos?
+El teorema de Pitágoras (a² + b² = c²) solo se usa en triángulos rectángulos para calcular la longitud de cualquier lado cuando conoces los otros dos. También puedes usarlo para verificar si un triángulo es rectángulo: si cumple la relación, entonces tiene un ángulo de 90°.