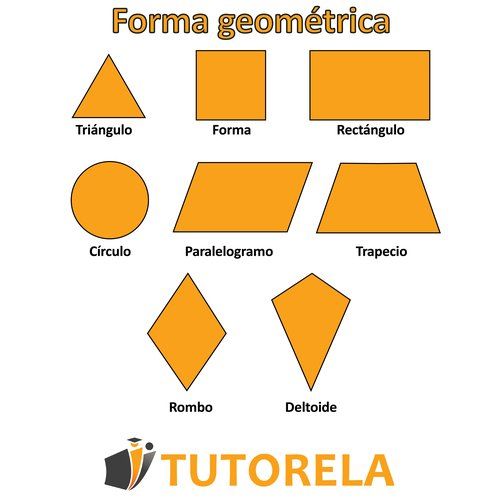
Hay una amplia variedad de formas geométricas, sobre las cuales puedes leer en detalle:
Figuras geométricas
¡Pruébate en triángulo!
Dado el deltoide de la figura:
¿Cuál es el área?
Formas geométricas
Triángulo
Un triángulo es una figura geométrica con lados. En todo triángulo, la suma de los ángulos es igual a .
A continuación se muestran los diferentes tipos de triángulos –
- Triángulo equilátero - un triángulo en el que todos los lados son iguales, todos los ángulos son iguales, y cada altura es también una mediana y una bisectriz.
- Triángulo isósceles - un triángulo en el que dos lados son iguales, dos ángulos de la base son iguales, y la mediana a la base es también la altura y la bisectriz del ángulo del vértice.
- Triángulo rectángulo - un triángulo con un ángulo de grados formado por dos catetos. El lado opuesto al ángulo recto se llama hipotenusa.
- Triángulo escaleno - un triángulo en el que todos los lados son diferentes entre sí.
Haz clic aquí para aprender más sobre triángulos.
Rectángulo
Un rectángulo es un cuadrilátero con dos pares de lados opuestos paralelos.
También se puede definir como un paralelogramo con un ángulo de grados.
Como un rectángulo es un tipo de paralelogramo, tiene todas las propiedades de un paralelogramo.
Aquí están las propiedades de un rectángulo:
- Cada par de lados opuestos son iguales y paralelos.
- Todos los ángulos en un rectángulo son iguales a grados.
- Las diagonales de un rectángulo son iguales entre sí.
- Las diagonales de un rectángulo se bisecan entre sí (se dividen una a la otra por la mitad, no solo se intersectan).
- Como ambas diagonales son iguales, todas las mitades de las diagonales son iguales.
- Las diagonales de un rectángulo no son perpendiculares entre sí y no bisecan los ángulos del rectángulo.
Haz clic aquí para aprender más sobre rectángulos.
Dado el rectángulo ABCD que tiene el lado AB de largo 4.5 cm y el lado BC de largo 2 cm.
¿Cuál es el área del rectángulo?
Dado el trapecio:
¿Cuál es el área?
Dado el rectángulo que tiene un lado AB de largo 2 cm y el lado BC de largo 7 cm.
¿Cuál es el perímetro del rectángulo?
Trapezoide
Un trapecio general es un trapecio donde dos de sus lados opuestos son paralelos y se llaman las bases del trapecio.
Los otros dos lados se llaman las piernas del trapecio, y no son paralelos y tienen direcciones diferentes.
Conoce las propiedades básicas de un trapecio:
• Dos lados son paralelos entre sí
• La suma de los ángulos que se apoyan en la misma pierna (uno de la base pequeña y otro de la base grande) es grados.
• Si trazamos una diagonal que intersecta ambas bases, creará ángulos alternos iguales entre líneas paralelas.
• La suma de todos los ángulos en un trapecio es igual a grados.
• Si trazamos un segmento que pasa exactamente por el medio de las piernas del trapecio, obtenemos un segmento que es paralelo a las bases e igual a la mitad de su suma.
¡Haz clic aquí para aprender más sobre los trapecios!
Paralelogramo
Un paralelogramo es un cuadrilátero con pares de lados paralelos.
Cómo comprobar un paralelogramo:
- Primera forma:
Si en un cuadrilátero cada par de lados opuestos son paralelos entre sí, el cuadrilátero es un paralelogramo. - Segunda forma:
Si en un cuadrilátero cada par de lados opuestos son iguales entre sí, el cuadrilátero es un paralelogramo. - Tercera forma:
Si en un cuadrilátero hay un par de lados opuestos que son tanto iguales como paralelos, el cuadrilátero es un paralelogramo. - Cuarta forma:
Si en un cuadrilátero, las diagonales se bisecan entre sí, el cuadrilátero es un paralelogramo. - Quinta forma:
Si en un cuadrilátero hay dos pares de ángulos opuestos iguales, el cuadrilátero es un paralelogramo.
¡Haz clic aquí para aprender más sobre paralelogramos!
Dado el trapecio de la figura
Halla su perímetro:
Dado el trapecio de la figura, ¿cuál es su perímetro?
Dado el rombo del dibujo:
¿Cuál es el área?
Deltoide
Un deltoide es un cuadrilátero con dos pares de lados adyacentes iguales.
Para entender esto mejor, imagina que un deltoide está compuesto por dos triángulos isósceles unidos.
Aquí están las propiedades principales del deltoide:
La diagonal principal en un cometa, que se extiende desde los dos vértices de los triángulos, es al mismo tiempo bisectriz del ángulo, mediana y perpendicular a la diagonal secundaria, que se extiende desde los ángulos de la base de los triángulos.
Haz clic aquí para aprender más sobre cometas.
Rombo
Un rombo es un paralelogramo con un par de lados adyacentes que son iguales.
Aquí están las propiedades de un rombo:
- En un rombo, todos los lados son iguales.
- En un rombo, hay dos pares de lados opuestos paralelos.
- En un rombo, los ángulos adyacentes suman grados.
- La suma de los ángulos es grados.
- En un rombo, hay dos pares de ángulos opuestos iguales.
Haz clic aquí para aprender más sobre el rombo.
Dado el rectángulo que tiene un lado DC de largo 1.5 cm y el lado AD de largo 9.5 cm.
¿Cuál es el perímetro del rectángulo?
Dado el trapecio ABCD
Dado en cm: AB=2.5 base DC=4 altura h=6
Calcula el área del trapecio
Dado el rombo del dibujo:
¿Cuál es el área?
ejemplos con soluciones para Triángulo
Ejercicio #1
Dado el trapecio:
¿Cuál es el área?
Solución en video
Solución Paso a Paso
Fórmula del área de un trapecio:
Reemplazamos los datos en la fórmula y resolvemos:
Respuesta
52.5
Ejercicio #2
Dado el trapecio ABCD
Dado en cm: AB=2.5 base DC=4 altura h=6
Calcula el área del trapecio
Solución en video
Solución Paso a Paso
Primero recordemos la fórmula del área del trapecio:
Reemplazamos los datos en la fórmula:
(2.5+4)*6 =
6.5*6=
39/2 =
19.5
Respuesta
Ejercicio #3
Dado el deltoide ABCD
La diagonal AC=8 es el área del deltoide es 32 cm²
Calcula la diagonal DB
Solución en video
Solución Paso a Paso
Primero, recordamos la fórmula del área del deltoide: multiplicar las longitudes de las diagonales entre sí y dividir este producto por 2.
Reemplazamos los datos sabidos en la fórmula:
Simplificamos el 8 y el 2:
Dividimos por 4
Respuesta
8 cm
Ejercicio #4
Dado el trapecio de la figura, ¿cuál es su perímetro?
Solución en video
Solución Paso a Paso
Para hallar el perímetro sumaremos todos los lados:
Respuesta
24
Ejercicio #5
¿Cuál es el área del trapecio de la figura?
Solución en video
Solución Paso a Paso
Usamos la fórmula para calcular el área de un trapecio: (base+base) multiplicado por la altura dividido por 2:
Respuesta
cm²
- El Teorema de Pitágoras
- La aplicación del teorema de Pitágoras en un ortoedro o cuboide
- Altura del triángulo
- Triángulos congruentes
- Criterio de congruencia: Lado, Ángulo, Lado
- Criterio de congruencia: Ángulo, Lado, Ángulo
- Criterio de congruencia: Lado, Lado, Lado
- Congruencia de triángulos rectángulos (en el contexto del Teorema de Pitágoras)
- Deltoide
- Área del deltoide:
- Suma de los ángulos internos de un triángulo
- Los lados o aristas de un triángulo
- Paralelogramo
- El área del paralelogramo: ¿qué es y cómo se calcula?
- Perímetro de un paralelogramo
- Semejanza de triángulos y polígonos
- Semejanza de figuras geométricas
- Razón de semejanza
- Triángulos semejantes
- Criterios de semejanza de triángulos
- Trapecios
- Simetría en trapecios
- Diagonales de un trapecio isósceles
- Área de un trapecio
- Perímetro de un trapecio
- Trapecio isósceles
- Rectángulo
- De un cuadrilátero a un rectángulo
- Del paralelogramo al rectángulo
- ¿Cómo se calcula el área de un rectángulo?
- El perímetro del rectángulo
- Rectángulos congruentes
- Ángulo exterior de un triángulo
- Relaciones entre ángulos y lados del triángulo
- La relación entre las longitudes de los lados de un triángulo
- Área
- ¿Rombo, cometa o diamante?
- Diagonales de un rombo
- Simetría del rombo
- De paralelogramo a rombo
- El área de un rombo
- Perímetro
- Triángulo
- Tipos de triángulos
- Triángulo obtuso
- Triángulo equilátero
- Identificación de un triángulo isósceles
- Triángulo escaleno
- Triángulo agudo
- Triángulo isósceles
- Área de un triángulo
- Área de un triángulo rectángulo
- Área del triángulo isósceles
- Área del triángulo escaleno
- Área del triángulo equilátero
- Perímetro de un triángulo
- Prisma triangular recto
- Las bases del prisma triangular recto
- Las caras laterales del prisma
- Aristas laterales de un prisma
- Altura del prisma
- El volumen del prisma
- Área de superficie de prismas triangulares
- Áreas de Polígonos para 7º Grado
- Triángulo Rectángulo
- Área de un trapecio rectángulo
- Área de un trapecio isósceles
- Mediana en un triángulo
- Centro de un Triángulo - El Centroide - El Punto de Intersección de las Medianas
- ¿Cómo calculamos el área de figuras complejas?
- ¿Cómo calculamos el perímetro de los polígonos?
- Todos los términos en el cálculo de triángulos
- ¿Cómo calcular el área de un triángulo usando trigonometría?
- Orden de operaciones básicas: suma, resta, multiplicación y división
- Orden de las operaciones básicas (potencias)
- Orden de operaciones básicas: raíces
- El 0 y el 1 en el orden de las operaciones
- Inverso multiplicativo
- Orden de las operaciones: paréntesis
- La propiedad conmutativa
- La propiedad asociativa
- Cómo calcular el área de un ortoedro
- Potenciación de números enteros
- Las Tablas de Multiplicar
- Fracciones