Valor absoluto

Si tenemos una incógnita o una expresión con una incógnita dentro de un valor absoluto, nos preguntaremos qué expresión nos traerá el valor de la ecuación deseada, dividiremos en casos y descubriremos la incógnita.
Ejemplo en la ecuación:  $│x+7│=12$
Nos preguntaremos qué expresión en valor absoluto será igual a $12$.
La respuesta será $12$ o $-12$. (Tanto un valor absoluto es igual a $12$ como un $12$ absoluto es igual a $-12$).
Por lo tanto, tomaremos la expresión completa y la dividiremos en dos casos:
Primer caso:
$x+7=12$
Resolvemos:
$x=5$

Segundo caso:
$X+7=-12$
Resolvemos
$x=-19$

Por lo tanto, la solución del ejercicio es: $x=5,-19$

Ejemplos:

• el valor absoluto de $-7$ se representa de la siguiente manera: $|7|$;
• el valor absoluto de $+9$ se representa de la siguiente manera: $|9|$. 

No obstante, al escribir cálculos, lo haremos de la siguiente manera:

• $|-20|= 20$
• $|+13.6|=13.6$
• $|(+44)+(-5)|=|+39|=39$
• $|-9+6|=|-3|=3$
• $|-9|+6=9+6=15$
• $|(-56)|+(-13)=56+(-13)=43$
• $28+|4-9|=28+|-5|=28+5=33$

El valor absoluto de un número número negativo siempre será superior a él. 

El valor absoluto de un número número positivo siempre equivaldrá al número positivo. 

Ejemplos:

• $|-6|>-6$
• $|+6|=+6$

Rellena los espacios con uno de los siguientes símbolos: <, >, =. 

• $-4$,$~▯~$,$|-4|$
• $|-9|$,$~▯~$,$+6$
• $|-50|$,$~▯~$,$|+50|$
• $8+5$,$~▯~$,$|-14|$
• $|-5-5|$,$~▯~$,$4+5$
• $|+53|$,$~▯~$,$53$
• $|-3-2|$,$~▯~$,$|6-1|$
• $|14+(-8)|$,$~▯~$,$14+|-8|$
• $14+(-8)$,$~▯~$,$|+14|+(-8)$

Resuelve los siguientes ejercicios:

• $|-5+6|=$
• $22-|-53|=$
• $|15-19|+|-9-7|=$
• $|15-19-9|-7=$
• $15-|19-9-7|=$
• $9.7-|4.3+(-6)|=$
• $9.7-4.3+|-6|=$

¿Con que símbolo se representa el valor absoluto y que representa en la recta numérica?

El valor absoluto de indica con el siguiente símbolo $\left\vert\right\vert$

En la recta numérica representa la distancia qué hay de un número al cero.

Por ejemplo el $\left\vert-5\right\vert=5$

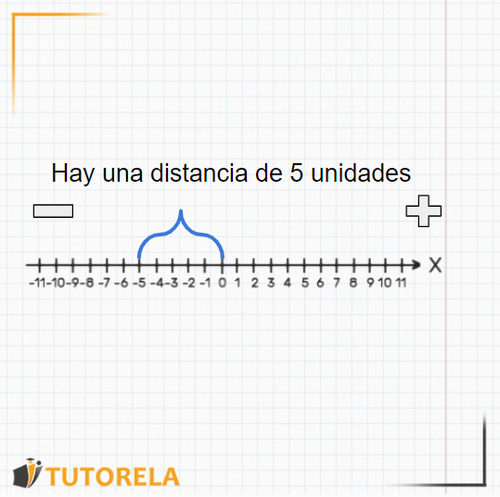
¿Qué es el valor absoluto?

El valor absoluto de un número será la distancia absoluta que hay entre ese número y el cero. Siempre el valor absoluto de un número positivo será una magnitud absoluta positiva y el valor absoluto de un número negativo será la magnitud absoluta en positiva, es decir solo estamos midiendo la distancia que hay desde dicho número al cero.

Ejemplos:

$\left\vert-6\right\vert=6$

$\left\vert6\right\vert=6$

$\left\vert9\right\vert=9$

$\left\vert-9\right\vert=9$

$\left\vert-50\right\vert=50$

$\left\vert50\right\vert=50$

$\left\vert-3.5\right\vert=3.5$

$\left\vert3.5\right\vert=3.5$

$\left\vert-\frac{1}{2}\right\vert=\frac{1}{2}$

$\left\vert\frac{1}{2}\right\vert=\frac{1}{2}$

3 ejercicios simples de valor absoluto

Veamos algunos ejercicios cuando nos aparecen ecuaciones con valor absoluto, en este caso debemos de encontrar el valor de la incógnita que va adentro del valor absoluto para que se cumpla la igualdad.

Ejercicio 1

Encuentra el valor de $x$ en la siguiente ecuación:

$\left\vert x+4\right\vert=10$

Debemos recordar que podemos tener dos soluciones por la definición del valor absoluto, entonces partimos nuestra ecuación en dos:

$x+4=10$

Despejamos a $x$

$x=10-4$

$x=6$

Ahora la otra parte

$x+4=-10$

$x=-10-4$

$x=-14$

Por lo tanto la solución es $x=6$, $x=-14$

Ejercicio 2

Encuentra la solución en la siguiente ecuación:

$\left\vert2x\right\vert=18$

Solución. Nuevamente partimos nuestra ecuación en dos casos por definición de valor absoluto

Caso 1

$2x=18$

$x=\frac{18}{2}$

$x=9$

Caso 2

$2x=-18$

$x=\frac{-18}{2}$

$x=-9$

Por lo tanto la solución es $x=9$, $x=-9$

Ejercicio 3

Encuentra los valores de $x$ para la siguiente ecuación $\left\vert3x+5\right\vert=20$

Solución

Caso 1.

$3x+5=20$

$3x=20-5$

$3x=15$

$x=\frac{15}{3}$

$x=5$

Caso 2.

$3x+5=-20$

$3x=-20-5$

$3x=-25$

$x=\frac{-25}{3}$

Por lo tanto los valores de $x$ que cumplen la ecuación con valor absoluto es $x=5$, $x=\frac{-25}{3}$

Si te interesa este artículo también te pueden interesar los siguientes artículos:

Números positivos, negativos y el cero

Valor absoluto y desigualdad con valor absoluto

Desigualdad (con valor absoluto)

La recta real

Números opuestos

Eliminación de paréntesis en números reales

Suma y resta de números reales

Multiplicación y división de números reales

Tabla de valores

En la pagina web de Tutorela encontrarás una variedad de artículos sobre matemáticas.