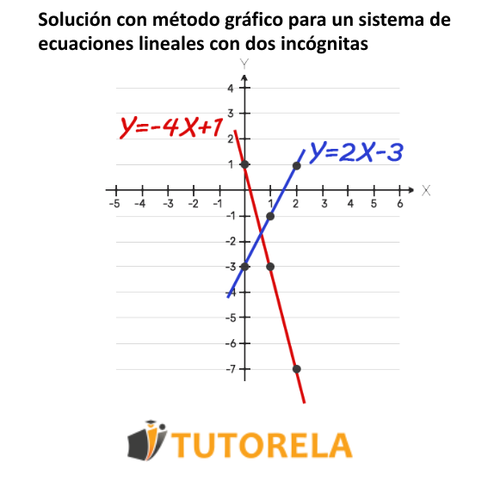
Para resolver con el método gráfico ecuaciones lineales que tienen dos incógnitas deberemos dibujar correctamente las dos gráficas sobre el plano cartesiano y hallar su punto de intersección.
¿Cómo lo haremos?
- Consideraremos cada ecuación como si fuera una función y haremos una tabla de valores de y de .
- Colocaremos en la de cada ecuación valores al azar (nosotros recomendamos poner ), luego deduciremos la correspondiente a cada y lo anotaremos respectivamente en la tabla de valores.
- Trazaremos un plano cartesiano y marcaremos en él los puntos de cada función.
- Luego de haber marcado todos los puntos de una función trazaremos una recta entre ellos y miraremos cómo se ve la función.
- Sólo después de esto comenzaremos a marcar los puntos de la segunda función para evitar confusión, seguidamente volveremos a trazar una recta entre estos últimos puntos.
- Analizaremos cuál es el punto de intersección entre las gráficas que dibujamos, este punto representa la solución de manera gráfica para tu sistema de ecuaciones lineales.
Nota que podrías ver un caso en el cual las rectas sean paralelas y, por lo tanto, no haya puntos de intersección entre ellas o bien, un caso en el cual las rectas se superpongan y, de este modo, habría puntos de intersección infinitos.