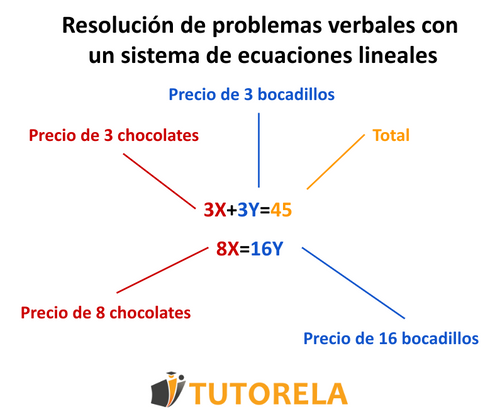
Para resolver problemas verbales con sistemas de ecuaciones lineales construiremos el sistema de ecuaciones basándonos en el texto del problema.
- Comenzaremos señalando lo que se nos pide despejar en las incógnitas y .
- Basándonos en las condiciones que cumplen y en el problema verbal anotaremos las ecuaciones pertinentes con los números y las incógnitas correspondientes.
- Luego de trazar las ecuaciones adecuadas al problema, podremos resolverlas del modo algebraico: a través del método de sustitución o bien del método de igualación, de esta manera despejaremos las dos incógnitas.