El triángulo obtuso es un triángulo que posee un ángulo obtuso (mayor de grados y menor de grados) y dos ángulos agudos (que cada uno de ellos es inferior a grados). El resultado de la suma de los tres ángulos juntos es grados.
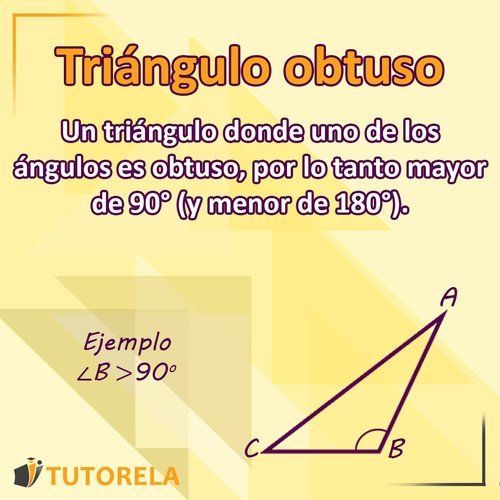
El triángulo obtuso es un triángulo que posee un ángulo obtuso (mayor de grados y menor de grados) y dos ángulos agudos (que cada uno de ellos es inferior a grados). El resultado de la suma de los tres ángulos juntos es grados.

En un triángulo rectángulo, ¿el lado opuesto al ángulo recto se llama?
A continuación, veremos algunos ejemplos de triángulos obtusos:
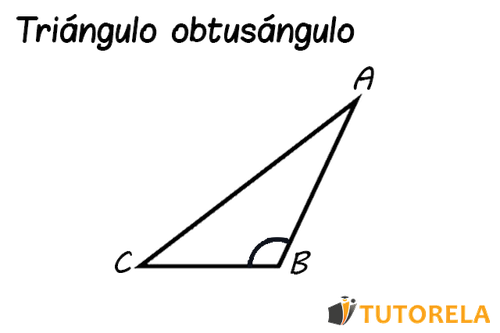
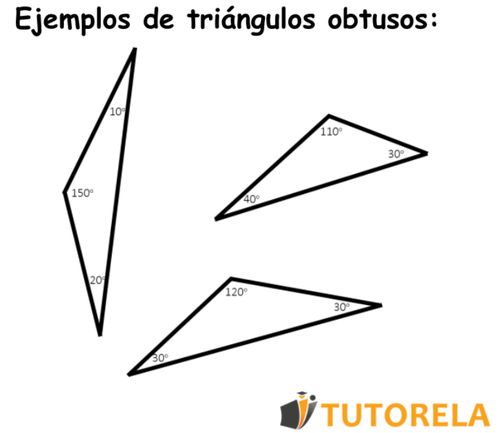
Si está interesado en aprender más sobre otros temas de triángulos, puede ingresar a uno de los siguientes artículos:
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Tarea:
Calcular cuál es más grande
Dado que el triángulo es un triángulo obtusángulo.
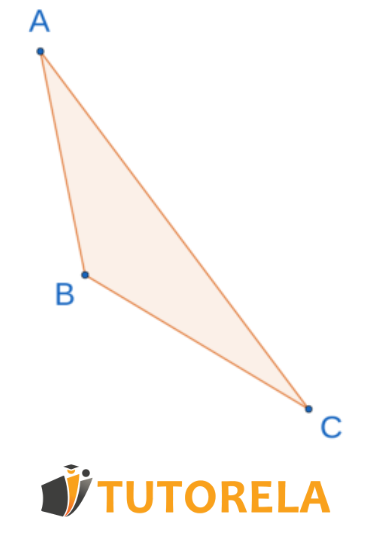
¿Qué ángulo es más grande o ?
Solución:
Como se nos da que el triángulo es un triángulo obtusángulo entendemos que es mayor que .
En un triángulo hay un solo ángulo obtuso por lo tanto la respuesta es:
Respuesta:
En un triángulo rectángulo, ¿cada uno de los dos lados que forman el ángulo recto se llama?
En un triángulo isósceles, ¿cada uno de los dos lados iguales se llama ?
En un triángulo isósceles, el ángulo entre dos ? se llama "ángulo ?"
Dado el triángulo .
obtuso.
La suma de los ángulos agudos en el triángulo es igual a .
Encontrar el valor del ángulo .
Solución:
Debido a que sabemos que es obtuso tenemos la certeza que los ángulos y son agudos.
Quiere decir que tenemos el dato que la suma de los ángulos agudos
La suma de los ángulos en el triángulo es igual a .
Respuesta:
Dado el triángulo obtusángulo .
,
Tarea:
¿Es posible calcular a ?
En caso que si, calcularlo.
Solución:
Dado que:
Reemplazamos:
Respuesta: si, .
¿El triángulo del dibujo es un triángulo rectángulo?
¿El dibujo muestra un triángulo obtuso?
¿El dibujo muestra un triángulo obtuso?
Consigna
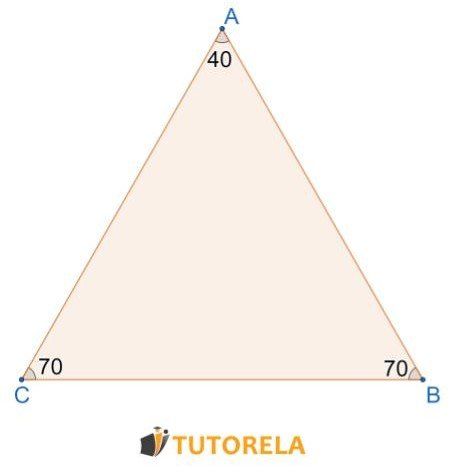
¿Qué triángulo fue dado en el dibujo?
Solución
Como los ángulos y : son ambos iguales , sabemos que los lados opuestos también son iguales, por lo tanto el triángulo es isósceles.
Respuesta
Triángulo isósceles
Consigna
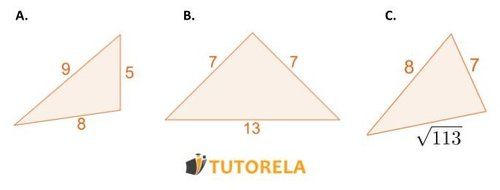
Determine cuál de los siguientes triángulos es obtuso, cuál es agudo y cuál es recto:
Solución
Observemos el triángulo y comprobemos si en él se cumple el teorema de pitágoras, en consecuencia reemplazamos los datos que tenemos:
Resolvemos la ecuación
La suma de los cuadrados de la "perpendicular" es mayor que el cuadrado del resto, por lo tanto el triángulo es un triángulo isósceles.
Observemos el triángulo y comprobemos si en él se cumple el teorema de pitágoras,en consecuencia reemplazamos los datos que tenemos:
Resolvemos la ecuación
La suma de los cuadrados de la "perpendicular" es menor que el cuadrado de la otra, por lo tanto el triángulo es obtuso
Observemos el triángulo y comprobemos si se cumple el teorema de pitágoras, primero calculamos a cuánto es igual la raíz de
Este es el lado más grande entre los: y nos referiremos a él como "hipotenusa".
Ahora reemplazamos los datos que tenemos:
Resolvemos la ecuación
En este triángulo se cumple el teorema de pitágoras y por lo tanto el triángulo es recto.
Respuesta
A: ángulo agudo B: ángulo obtuso C: ángulo recto
Dados los valores de los lados de un triángulo, ¿es un triángulo con lados diferentes?
Dados los valores de los lados de un triángulo, ¿es un triángulo con lados diferentes?
¿El triángulo del dibujo es un triángulo acutángulo?
¿El triángulo del dibujo es un triángulo rectángulo?
Se puede observar que todos los ángulos en el triángulo dado son menores de 90 grados.
En un triángulo rectángulo debe haber un ángulo igual a 90 grados.
Como este dato no existe, el triángulo no es un triángulo rectángulo.
No
En un triángulo rectángulo, ¿la suma de los dos ángulos no rectos es ?
En un triángulo rectángulo hay un ángulo igual a 90 grados, los otros dos ángulos suman 90 grados (180° es la suma de los ángulos en un triángulo)
Por lo tanto, la suma de los dos ángulos no rectos es 90 grados.
90 grados
Elija el triángulo apropiado según la figura:
Ángulo B es igual a 90 grados
Tengamos en cuenta que los triángulos en el ángulo B forma un ángulo recto, es decir, un ángulo de 90 grados.
En las respuestas c+d puedes ver que el ángulo B es menor a 90 grados.
La respuesta a es igual a 90 grados.
Cuál triángulo es el siguiente
Dado que en un triángulo obtusángulo basta con que uno de los ángulos sea mayor que 90°, y en el triángulo dado tenemos un ángulo C mayor que 90°,
Además, la suma de los ángulos del triángulo dado es 180 grados:
El triángulo es obtusángulo.
Triángulo obtusángulo
¿Qué triángulo se da en el dibujo?
La medida del ángulo C es de 90°, por lo tanto es un ángulo recto.
Si uno de los ángulos del triángulo es recto, es un triángulo rectángulo.
Triángulo rectángulo