En síntesis: LLA
Significa que:
si dos triángulos tienen dos lados iguales y también es igual el ángulo opuesto al mayor de los dos lados, los triángulos son congruentes.
En síntesis: LLA
Significa que:
si dos triángulos tienen dos lados iguales y también es igual el ángulo opuesto al mayor de los dos lados, los triángulos son congruentes.

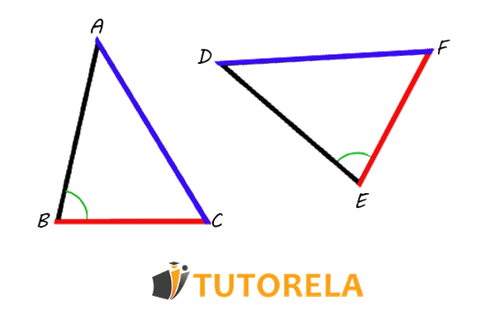
Dados los triángulos del dibujo
¿Cuál de las afirmaciones es necesariamente verdadera?
Ha llegado la hora de estudiar el cuarto teorema de congruencia: Lado, lado y el ángulo opuesto al mayor de los dos lados
o abreviando:
LLA
este teorema de congruencia es práctico y cómodo, y nos ayudará a demostrar la congruencia en triángulos bajo ciertas condiciones sencillas.
¿Qué dice el teorema de congruencia Lado, lado y el ángulo opuesto al mayor de los dos lados?
Si dos triángulos tienen dos lados iguales y también es igual el ángulo opuesto al mayor de los dos lados, los triángulos son congruentes.
¿Qué quiere decir?
Veámoslo en una ilustración:

Si tenemos:
y también:
Es decir, los triángulos tienen dos lados iguales,
y también:
cuando
Es decir, también el ángulo opuesto al mayor de los lados es igual.
Podemos determinar que los triángulos son congruentes según el teorema LLA
Pon atención en que, a pesar de que está dado en sólo un triángulo
pero, ya que tenemos un dato previo que dice que:
y también:
podremos determinar acorde a la relación transitiva que también:
Por lo tanto, determinaremos que:
Observa que hemos escrito la congruencia en el orden correcto.
Cuando
Ya que los triángulos son congruentes, idénticos en sus lados y en sus ángulos podremos decir que:
Recuerda que deben ocurrir 3 circunstancias y una condición:
Las 3 circunstancias requeridas son:
La condición:
Dados los triángulos del dibujo
¿Cuál de las afirmaciones es verdadera?
Dados los triángulos del dibujo
Determina cuál de las afirmaciones es correcta:
Dados los triángulos del dibujo
¿Cuál de las siguientes afirmaciones es necesariamente verdadera?
Veamos algunas maneras de hacerlo:
Si te interesa este artículo también te pueden interesar los siguientes artículos:
Criterio de congruencia: Lado, Ángulo, Lado
Criterio de congruencia: Ángulo, Lado, Ángulo
Criterio de congruencia: Lado, Lado, Lado
Modo de escritura de la demostración formal en geometría
En la página web de Tutorela encontrarás una variedad de artículos sobre matemáticas.
Consigna
Dado: el cuadrilátero es un paralelogramo.
¿Según qué teorema de congruencia los triángulos se superponen?
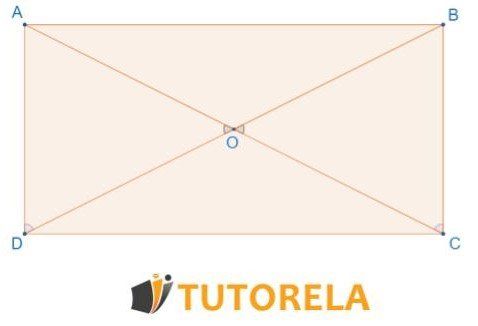
Solución
Dado que el cuadrilátero es un rectángulo, en el rectángulo hay dos pares de lados paralelos iguales, por lo tanto:
Ángulos alternos entre rectas paralelas son iguales, por lo tanto:
Ángulos opuestos por el vértice iguales, y por lo tanto:
Comprobamos que los triángulos congruentes según el teorema de lado, ángulo, ángulo.
Respuesta:
Congruentes según A.L.A
Dados los triángulos del dibujo
¿De acuerdo con qué teorema, los triángulos son congruentes?
¿Qué dato se debe agregar para que los triángulos sean congruentes?
¿Qué dato se debe agregar para que los triángulos sean congruentes?
Consigna
¿ no es un lado en ninguno de los triángulos?
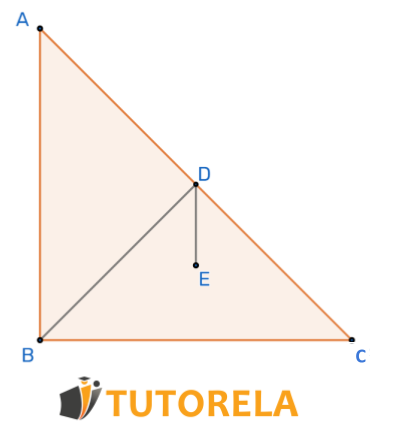
Solución
Si miramos el gráfico vemos que desde un punto sale un línea al punto por lo tanto es una línea recta que no es un lado de ningún triángulo en el dibujo.
Respuesta
Verdadero
Consigna
En el dibujo dado:
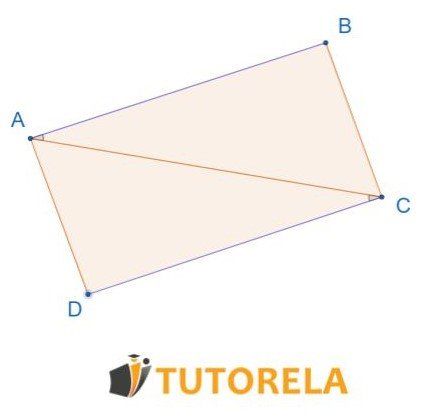
¿Según qué teorema de congruencia coinciden los triángulos ?
Solución
Dado que
Dado que
es el lado común
Comprobamos que los triángulos son congruentes según lado, ángulo, lado
Respuesta
Congruentes según L.A.L
¿Cuáles de los triángulos son congruentes?
¿Son congruentes los triángulos de la imagen?
¿Qué dato se debe agregar para que los triángulos sean congruentes?

Consigna
Dado el rectángulo de lado de longitud de cm y el lado de longitud cm.
¿Cuál es el área del rectángulo?
Solución
La fórmula de cálculo del área rectangular es la base multiplicada por la altura, en este caso reemplazamos
Respuesta
Consigna
Los segmentos y se cruzan en el punto .
¿Según qué teorema de congruencia coinciden los triángulos ?
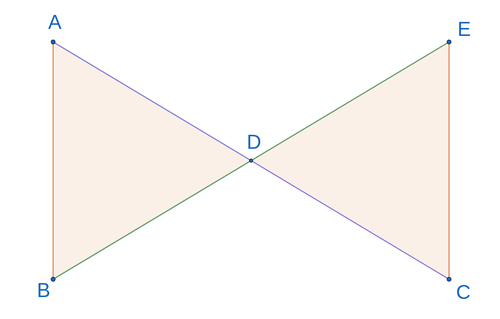
Solución
y
Se cruzan en un punto
intersecta
Ángulos opuestos por el vértice
Triángulos superpuestos según
Respuesta
Superpuestos
¿Los triángulos son congruentes?
¿Los triángulos son congruentes?
¿Son congruentes los triángulos de la imagen?
Dados los triángulos del dibujo
¿Cuál de las afirmaciones es verdadera?
Esta pregunta en realidad tiene dos pasos:
En el primer paso, debe definir si los triángulos son congruentes o no,
y luego identificar la respuesta correcta entre las opciones.
Observemos los triángulos: tenemos dos lados iguales y un ángulo,
Pero este no es el ángulo entre ellos, por lo tanto, no se puede probar de acuerdo con el teorema de L.A.L
Recuerda el cuarto teorema de congruencia - L.L.A
Si los dos triángulos son iguales entre sí en cuanto a las longitudes de los dos lados y el ángulo opuesto al lado que es el mayor, entonces los triángulos son congruentes.
Pero el ángulo que tenemos no es opuesto al lado mayor, sino al lado menor,
Por lo tanto, no es posible probar que los triángulos son congruentes y no se puede establecer ningún teorema.
No es posible calcular
Dados los triángulos del dibujo
Determina cuál de las afirmaciones es correcta:
Tengamos en cuenta que:
AC=EF=4
DF=AB=5
Como 5 es mayor que 4 y el ángulo igual a 34 es opuesto al lado mayor en ambos triángulos, entonces el ángulo ACB es igual al ángulo DEF
Por lo tanto, los triángulos son congruentes según el teorema L.L.A, como resultado de esto todos los ángulos y lados son congruentes, y todas las respuestas son correctas.
Todas las respuestas son correctas
Dados los triángulos del dibujo
¿Cuál de las siguientes afirmaciones es necesariamente verdadera?
De acuerdo con los datos existentes:
(Lado)
(Lado)
Los ángulos iguales a 53 grados son ambos opuestos al lado mayor (que es igual a 13) en ambos triángulos.
(Ángulo)
Puesto que los lados y los ángulos son iguales entre triángulos congruentes, se puede determinar que el ángulo DEF es igual al ángulo BAC
Ángulos BAC es igual al ángulo DEF
¿Qué dato se debe agregar para que los triángulos sean congruentes?
Tengamos en cuenta que:
DF=AC=8
DE=AB=5
8 es mayor que 5, por lo tanto el ángulo DEF es opuesto al lado mayor y es igual a 65 grados.
Es decir, la figura que nos falta es el ángulo del segundo triángulo.
Examinaremos qué ángulo está opuesto al lado grande AC.
ABC es el ángulo opuesto al lado mayor AC por lo que debe ser igual a 65 grados.
Ángulo ABC es igual a 65
¿Cuáles de los triángulos son congruentes?
Observemos el ángulo en cada uno de los triángulos y notemos que cada vez es opuesto a la longitud de un lado diferente.
Por lo tanto, ninguno de los triángulos es congruente ya que es imposible saberlo a partir de los datos.
No es posible saber según los datos