Gráfica discreta

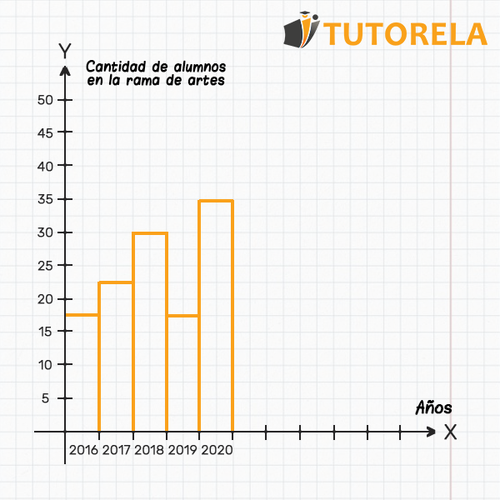
• En este diagrama discreto, los años se colocan en el eje $X$, mientras que en el eje $Y$ están la cantidad de estudiantes que se especializaron en artes en una escuela en particular.
• Cada columna está por separado y no forma una secuencia de columnas antes o después de ella.
• Mediante este diagrama de barras, es posible tener una representación discreta, en donde podemos visualizar una impresión de los cambios que han tenido lugar a lo largo de los años en la cantidad de estudiantes en la rama de artes, pero no existe una secuencia numérica entre estos valores.

Si estás interesado en más información sobre "gráficos" puedes encontrar información detallada en los siguientes artículos:

Recolección y organización de datos - investigación estadística

Lectura de información de gráficos

Grafico

Gráfica continua

Representación gráfica de una función

En la página web de Tutorela encontrarás una variedad de artículos con interesantes explicaciones sobre matemáticas

A veces las gráficas parecen complicadas, pero si entendemos cómo funcionan veremos que, en realidad, son muy simples. Una gráfica es sólo una manera de mostrar mucha información de una vez.

Tenemos varios tipos básicos de gráficas. En este artículo conoceremos las gráficas discretas. Para entender cómo actúan comenzaremos con un ejemplo. En el ejemplo que se expone a continuación podrás ver una gráfica que representa la cantidad de alumnos que cursaron Arte en cada año lectivo.

Toda gráfica se compone de dos ejes: el eje $X$ y el eje $Y$. El eje $X$ es el horizontal (podemos imaginarlo como el suelo de la gráfica). En esta gráfica nos está indicando los años, tal como se explicita. El eje $Y$ es el vertical (podemos imaginarlo como la pared de la gráfica). En esta gráfica nos está indicando la cantidad de alumnos que estudian arte, tal como aparece escrito a su lado, en el título: $5, 10, 15,$ etc. hasta $50$.

En este artículo aprenderemos a analizar la gráfica de la función.

Este es un claro ejemplo de un gráfico de datos discretos, toda gráfica se compone de dos ejes: el eje $X$ y el eje $Y$. El eje $X$ es el horizontal (podemos imaginarlo como el suelo de la gráfica). En una gráfica discreta como la nuestra, el eje $X$ representará distintas categorías. Observemos el ejemplo que tenemos. Intenta identificar el eje $X$, aparece señalizado con dicha letra.

En este caso el eje $X$ indica la categoría Años, tal como lo describe, a su derecha, el título. Podemos ver los años escritos en la gráfica debajo de cada columna: $2016, 2017$ y así sucesivamente.

El eje $Y$ es el vertical (podemos imaginarlo como la pared de la gráfica). En esta gráfica nos está indicando la cantidad de alumnos que estudian arte, tal como aparece escrito a su lado, en el título: $5, 10, 15,$ etc. hasta $50$.

A través de esta gráfica interpretaremos cuántos alumnos estudiaron Arte cada año. Esta información está representada en las columnas.

Por ejemplo, observemos el eje $X$ en el año $2018$. Vemos que sobre el año $2018$ hay una columna anaranjada que se eleva hasta el número $30$ del eje $Y$. Esto significa que en el año $2018$ $30$ alumnos exactamente estudiaron Arte.

Otro ejemplo, observemos el eje $X$ en el año $2020$. La columna sobre $2020$ se eleva exactamente hasta el número 35 del eje $Y$. Es decir, en el año $2020$ $35$ alumnos exactamente estudiaron Arte.

Ahora, inténtalo tú, veamos si descubres cuántos alumnos cursaron Arte en el año $2017$. Identifica el año solicitado sobre el eje $X$. Ahora te percatarás de que la columna que se eleva desde el año $2017$ no llega a un punto claramente señalado sobre el eje $Y$. Sin embargo, podemos ver que la gráfica llega aproximadamente a un punto medio entre el $20$ y el $25$. O sea, probablemente se trate de $22$ o $23$ alumnos (ya que no puede ser $22.5$ alumnos, sería imposible pensar en medio alumno).

Aunque la respuesta exacta no quede totalmente clara, es suficiente para nosotros. Nos alcanzará con saber que se trata de $22$ o $23$ alumnos. Ésta es la información que podemos deducir de esta gráfica tal como está. Si la gráfica de la función estuviera más detallada podríamos deducir con exactitud cuántos alumnos estudiaron Arte en el año $2017$.

El motivo de la denominación usada para este tipo de gráficas «gráfica discreta» se debe a que cada categoría actúa «a su propia discreción» y sin relación con las demás. No hay continuidad entre las categorías, cada columna es independiente y ajena a las contiguas. Seguidamente veremos una gráfica de otro tipo, gráfica continua.